
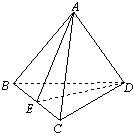
 已知:空間四邊形ABCD,AB=AC,DB=DC,
已知:空間四邊形ABCD,AB=AC,DB=DC,科目:高中數學 來源: 題型:
 已知在空間四邊形ABCD中,E、F分別是AB、AD的中點,G、H分別是BC、CD上的點,且BG:GC=DH:HC=2:1,則EG、FH、AC的位置關系是( )
已知在空間四邊形ABCD中,E、F分別是AB、AD的中點,G、H分別是BC、CD上的點,且BG:GC=DH:HC=2:1,則EG、FH、AC的位置關系是( )| A、兩兩異面 | B、兩兩平行 | C、交于一點 | D、兩兩相交 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 7 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 (2011•順義區一模)如圖,已知在空間四邊形ABCD中,AB=AC=DB=DC,E為BC的中點.
(2011•順義區一模)如圖,已知在空間四邊形ABCD中,AB=AC=DB=DC,E為BC的中點.查看答案和解析>>
科目:高中數學 來源:2010年北京市高一下學期期末考試數學卷 題型:解答題
(本小題9分)已知:空間四邊形ABCD,E,F,G,H分別是AB,BC,CD,DA的中點,BD=AC.求證:四邊形EFGH是菱形。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com