
已知函數![]() 的極小值大于零,其中
的極小值大于零,其中![]() ,
,![]() .
.
(I)求![]() 的取值范圍;
的取值范圍;
(II)若在![]() 的取值范圍內的任意
的取值范圍內的任意![]() ,函數
,函數![]() 在區間
在區間![]() 內都是增函數,
內都是增函數,
求實數![]() 的取值范圍;
的取值范圍;
(III)設![]() ,
,![]() ,若
,若![]() ,求證:
,求證:![]() .
.
解:(I)![]() 令
令![]() 得
得![]()
函數![]() 存在極值,
存在極值,![]() , …………(1分)
, …………(1分)
由![]() 及(I),只需考慮
及(I),只需考慮![]() 的情況.當
的情況.當![]() 變化時,
變化時,![]() 的符號及
的符號及![]() 的變化情況如下表:
的變化情況如下表:
|
|
| 0 |
|
|
|
|
| + | 0 | - | 0 | + |
|
|
| 極大值 |
| 極小值 |
|
因此,函數![]() 在
在![]() 處取得極小值
處取得極小值![]() 且
且![]()
…………(3分)
要使![]() 必有
必有![]() 可得
可得![]()
所以![]() 的取值范圍是
的取值范圍是![]() …………(5分)
…………(5分)
(II)由(I)知,函數![]() 在區間
在區間![]() 與
與![]() 內都是增函數.
內都是增函數.
由題設,函數![]() 在
在![]() 內是增函數,則
內是增函數,則![]() 須滿足不等式組
須滿足不等式組
![]() ,或
,或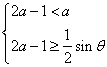 ,
,
∵![]() ∴要使不等式
∴要使不等式![]() 關于參數
關于參數![]() 恒成立,必有
恒成立,必有![]()
解得![]() 或
或![]() ,所以
,所以![]() 的取值范圍是
的取值范圍是![]() …………(10分)
…………(10分)
(III)用反證法證明:
假設![]() ,則
,則![]() ,或
,或![]() ,∵
,∵![]() ,
,![]() ,
,
∴![]() ,或
,或![]()
當![]() 時,∵函數
時,∵函數![]() 在區間
在區間![]() 內是增函數,
內是增函數,
∴![]() ,即
,即![]() 矛盾;
矛盾;
當![]() 時,∵函數
時,∵函數![]() 在區間
在區間![]() 內是增函數,
內是增函數,
∴![]() ,即
,即![]() 也矛盾;
也矛盾;
故假設不成立,即![]() 成立. …………(14分)
成立. …………(14分)


 全優點練單元計劃系列答案
全優點練單元計劃系列答案科目:高中數學 來源: 題型:
(06年天津卷文)(12分)
已知函數![]() 其中
其中![]() 為參數,且
為參數,且![]()
(I)當![]() 時,判斷函數
時,判斷函數![]() 是否有極值;
是否有極值;
(II)要使函數![]() 的極小值大于零,求參數
的極小值大于零,求參數![]() 的取值范圍;
的取值范圍;
(III)若對(II)中所求的取值范圍內的任意參數![]() ,函數
,函數![]() 在區間
在區間![]() 內都是增函數,求實數
內都是增函數,求實數![]() 的取值范圍。
的取值范圍。
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
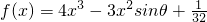 的極小值大于零,其中x∈R,θ∈[0,π].
的極小值大于零,其中x∈R,θ∈[0,π].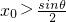 ,
,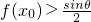 ,若f[f(x0)]=x0,求證:f(x0)=x0.
,若f[f(x0)]=x0,求證:f(x0)=x0.查看答案和解析>>
科目:高中數學 來源:2011年山東省煙臺市高考數學模擬試卷(文科)(解析版) 題型:解答題
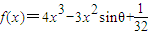 的極小值大于零,其中x∈R,θ∈[0,π].
的極小值大于零,其中x∈R,θ∈[0,π]. ,
,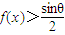 ,若f[f(x)]=x,求證:f(x)=x.
,若f[f(x)]=x,求證:f(x)=x.查看答案和解析>>
科目:高中數學 來源:2011年遼寧省丹東市高考數學模擬試卷(理科)(解析版) 題型:解答題
 的極小值大于零,其中x∈R,θ∈[0,π].
的極小值大于零,其中x∈R,θ∈[0,π].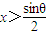 ,
, ,若f[f(x)]=x,求證:f(x)=x.
,若f[f(x)]=x,求證:f(x)=x.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com