【題目】下列函數中滿足在（﹣∞，0）上單調遞減的偶函數是（ ）
A.
B.y=|log2（﹣x）|
C.
D.y=sin|x|
【答案】C
【解析】解：對于A：根據指數函數的性質， 
的圖象是y= 
圖象把y軸的右邊圖象翻折后得左邊圖象，在（﹣∞，0）上單調遞增函數，∴A不對．
對于B：根據圖象，y=|log2（﹣x）|，在（﹣∞，﹣1）是減函數，（﹣1，0）是增函數，∴B不對．
對于C：根據冪函數的性質可知： 
是偶函數，指數 
，（0，+∞）是增函數．（﹣∞，0）上單調遞減．∴C對．
對于D：根據正弦函數的性質可知：y=sin|x|的圖象是由sinx在y軸的右邊圖象翻折后得左邊圖象．
故選：C．
【考點精析】解答此題的關鍵在于理解函數單調性的性質的相關知識，掌握函數的單調區間只能是其定義域的子區間 ,不能把單調性相同的區間和在一起寫成其并集．
天天向上一本好卷系列答案
小學生10分鐘應用題系列答案科目：高中數學 來源： 題型：
【題目】給出定義：若 
（其中m為整數），則m叫做離實數x最近的整數，記作{x}，即{x}=m在此基礎上給出下列關于函數f（x）=|x﹣{x}|的四個命題： ① 
；②f（3.4）=﹣0.4；
③ 
；④y=f（x）的定義域為R，值域是 
；
則其中真命題的序號是（ ）
A.①②
B.①③
C.②④
D.③④
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函數f（x）=4sinxcos2（ 
+ 
）﹣cos2x．
（1）將函數y=f（2x）的圖象向右平移 
個單位長度得到函數y=g（x）的圖象，求函數g（x）在x∈[ 
， 
]上的值域；
（2）已知a，b，c分別為△ABC中角A，B，C的對邊，且滿足b=2，f（A）= 
a=2bsinA，B∈（0， ），求△ABC的面積．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】設 
，曲線y=f（x）在點（1，f（1））處的切線與直線x+y+1=0垂直．
（1）求a的值；
（2）若對于任意的x∈[1，+∞），f（x）≤m（x﹣1）恒成立，求m的取值范圍．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】如圖，在多面體ABCDM中，△BCD是等邊三角形，△CMD是等腰直角三角形，∠CMD=90°，平面CMD⊥平面BCD，AB⊥平面BCD． 
（Ⅰ）求證：CD⊥AM；
（Ⅱ）若AM=BC=2，求直線AM與平面BDM所成角的正弦值．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知函f（x）=lnx﹣ax2+（2﹣a）x． ①討論f（x）的單調性；
②設a＞0，證明：當0＜x＜ 
時， 
；
③函數y=f（x）的圖象與x軸相交于A、B兩點，線段AB中點的橫坐標為x0 ， 證明f′（x0）＜0．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】在某單位的職工食堂中，食堂每天以3元/個的價格從面包店購進面包，然后以5元/個的價格出售．如果當天賣不完，剩下的面包以1元/個的價格賣給飼料加工廠．根據以往統計資料，得到食堂每天面包需求量的頻率分布直方圖如下圖所示．食堂某天購進了90個面包，以x（單位：個，60≤x≤110）表示面包的需求量，T（單位：元）表示利潤．
（Ⅰ）求T關于x的函數解析式；
（Ⅱ）根據直方圖估計利潤T不少于100元的概率；
（Ⅲ）在直方圖的需求量分組中，以各組的區間中點值代表該組的各個值，并以需求量落入該區間的頻率作為需求量取該區間中間值的概率（例如：若需求量x∈[60，70），則取x=65，且x=65的概率等于需求量落入[60，70）的頻率），求T的分布列和數學期望．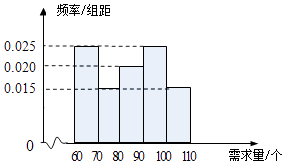
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知曲線C1的參數方程為 
（t為參數）．以坐標原點為極點，x軸的正半軸為極軸建立極坐標系，曲線C2的極坐標方程為ρ=2cosθ．
（Ⅰ）把C1的參數方程化為極坐標方程；
（Ⅱ）求C1與C2交點的極坐標（ρ≥0，0≤θ＜2π）．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
