
【題目】數學中有許多形狀優美寓意美好的曲線,曲線![]() 就是其中之一(如圖).給出下列三個結論:
就是其中之一(如圖).給出下列三個結論:

①曲線![]() 恰好經過6個整點(即橫縱坐標均為整數的點);
恰好經過6個整點(即橫縱坐標均為整數的點);
②曲線![]() 上存在到原點的距離超過
上存在到原點的距離超過![]() 的點;
的點;
③曲線![]() 所圍成的“心形”區域的面積小于3.
所圍成的“心形”區域的面積小于3.
其中,所有錯誤結論的序號是______.
【答案】②③
【解析】
將![]() 換成
換成![]() 方程不變,得到圖形關于
方程不變,得到圖形關于![]() 軸對稱,根據對稱性,分類討論,逐一判定,即可求解.
軸對稱,根據對稱性,分類討論,逐一判定,即可求解.
將![]() 換成
換成![]() 方程不變,所以圖形關于
方程不變,所以圖形關于![]() 軸對稱,
軸對稱,
當![]() 時,代入可得
時,代入可得![]() ,解得
,解得![]() ,即曲線經過點
,即曲線經過點![]() ,
,
當![]() 時,方程變換為
時,方程變換為![]() ,
,
由![]() ,解得
,解得![]() ,
,
所以![]() 只能去整數
只能去整數![]() ,當
,當![]() 時,
時,![]() ,解得
,解得![]() 或
或![]() ,即曲線經過
,即曲線經過![]() ,
,
根據對稱性可得曲線還經過![]() ,
,
所以曲線一共經過6個整點,所以①是正確的;
當![]() 時,由
時,由![]() ,可得
,可得![]() ,當且僅當
,當且僅當![]() 時取等號,
時取等號,
所以![]() ,所以
,所以![]() ,
,
即曲線C上![]() 軸右邊的點到原點的距離不超過
軸右邊的點到原點的距離不超過![]() ,
,
根據對稱性可得:曲線C上任意一點到原點的距離都不超過![]() ,所以②不正確;
,所以②不正確;
如圖所示,在![]() 軸上圖形的面積大于矩形
軸上圖形的面積大于矩形![]() 的面積:
的面積:![]() ,
,![]() 軸下方的面積大于等腰三角形
軸下方的面積大于等腰三角形![]() 的面積:
的面積:![]() ,所以曲線C所圍成的“心形”區域的面積大于
,所以曲線C所圍成的“心形”區域的面積大于![]() ,所以③不正確的.
,所以③不正確的.
故選:②③.



科目:高中數學 來源: 題型:
【題目】已知![]() 為橢圓
為橢圓![]() 上的一點,F為橢圓的右焦點,且
上的一點,F為橢圓的右焦點,且![]() 垂直于x軸,不過原點O的直線
垂直于x軸,不過原點O的直線![]() 交橢圓于A,B兩點,線段
交橢圓于A,B兩點,線段![]() 的中點M在直線
的中點M在直線![]() 上.
上.
(1)求橢圓C的標準方程;
(2)當![]() 的面積最大時,求直線
的面積最大時,求直線![]() 的方程.
的方程.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,直線l的參數方程為
中,直線l的參數方程為![]() (t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為
(t為參數),以坐標原點O為極點,x軸正半軸為極軸建立極坐標系,曲線C的極坐標方程為![]()
(1)求直線l的普通方程和曲線C的直角坐標方程;
(2)若直線l與曲線C相交于A,B兩點.求![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某飲料廠生產![]() 兩種飲料.生產1桶
兩種飲料.生產1桶![]() 飲料,需該特產原料100公斤,需時間3小時;生產1桶
飲料,需該特產原料100公斤,需時間3小時;生產1桶![]() 飲料需該特產原料100公斤,需時間1小時,每天
飲料需該特產原料100公斤,需時間1小時,每天![]() 飲料的產量不超過
飲料的產量不超過![]() 飲料產量的2倍,每天生產兩種飲料所需該特產原料的總量至多750公斤,每天生產
飲料產量的2倍,每天生產兩種飲料所需該特產原料的總量至多750公斤,每天生產![]() 飲料的時間不低于生產
飲料的時間不低于生產![]() 飲料的時間,每桶
飲料的時間,每桶![]() 飲料的利潤是每桶
飲料的利潤是每桶![]() 飲料利潤的1.5倍,若該飲料廠每天生產
飲料利潤的1.5倍,若該飲料廠每天生產![]() 飲料
飲料![]() 桶,
桶,![]() 飲料
飲料![]() 桶時(
桶時(![]() )利潤最大,則
)利潤最大,則![]() _____.
_____.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列{an}滿足:a1=0,![]() (n∈N*),前n項和為Sn (參考數據: ln2≈0.693,ln3≈1.099),則下列選項中錯誤的是( )
(n∈N*),前n項和為Sn (參考數據: ln2≈0.693,ln3≈1.099),則下列選項中錯誤的是( )
A.![]() 是單調遞增數列,
是單調遞增數列,![]() 是單調遞減數列B.
是單調遞減數列B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知正四棱錐![]() 的底面邊長為
的底面邊長為![]() 高為
高為![]() 其內切球與面
其內切球與面![]() 切于點
切于點![]() ,球面上與
,球面上與![]() 距離最近的點記為
距離最近的點記為![]() ,若平面
,若平面![]() 過點
過點![]() ,
,![]() 且與
且與![]() 平行,則平面
平行,則平面![]() 截該正四棱錐所得截面的面積為______.
截該正四棱錐所得截面的面積為______.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,正方體![]() 的棱長為1,線段
的棱長為1,線段![]() 上有兩個動點
上有兩個動點![]() ,且
,且![]() ,現有如下四個結論:
,現有如下四個結論:
![]() ;
;![]() 平面
平面![]() ;
;
![]() 三棱錐
三棱錐![]() 的體積為定值;
的體積為定值;![]() 異面直線
異面直線![]() 所成的角為定值,
所成的角為定值,
其中正確結論的序號是______.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() ABCD中,
ABCD中,![]() 和
和![]() 都是等邊三角形,平面PAD
都是等邊三角形,平面PAD![]() 平面ABCD,且
平面ABCD,且![]() ,
,![]() .
.
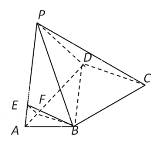
(1)求證:CD![]() PA;
PA;
(2)E,F分別是棱PA,AD上的點,當平面BEF//平面PCD時,求四棱錐![]() 的體積.
的體積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com