
【題目】已知a,b,c分別為△ABC中角A,B,C的對(duì)邊,函數(shù) ![]() 且f(A)=5.
且f(A)=5.
(1)求角A的大小;
(2)若a=2,求△ABC面積的最大值.
【答案】
(1)解:由題意可得: ![]()
=3+ ![]() sin2A+cos2A+1=4+2sin(2A+
sin2A+cos2A+1=4+2sin(2A+ ![]() ),
),
∴sin(2A+ ![]() )=
)= ![]() ,∵A∈(0,π),
,∵A∈(0,π),
∴2A+ ![]() ∈(
∈( ![]() ,
, ![]() ),∴2A+
),∴2A+ ![]() =
= ![]() ,∴A=
,∴A= ![]()
(2)解:由余弦定理可得: ![]() ,
,
即4=b2+c2﹣bc≥bc(當(dāng)且僅當(dāng)b=c=2時(shí)“=”成立),即bc≤4,
∴ ![]() ,
,
故△ABC面積的最大值是 ![]()
【解析】(1)利用三角恒等變換求得f(A)的解析式,由f(A)=5求得 sin(2A+ ![]() ) 的值,從而求得2A+
) 的值,從而求得2A+ ![]() 的值,可得A的值.(2)利用余弦定理,基本不等式,求得bc的最大值,可得△ABC面積
的值,可得A的值.(2)利用余弦定理,基本不等式,求得bc的最大值,可得△ABC面積 ![]() bcsinA的最大值.
bcsinA的最大值.
【考點(diǎn)精析】利用余弦定理的定義對(duì)題目進(jìn)行判斷即可得到答案,需要熟知余弦定理:![]() ;
;![]() ;
;![]() .
.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,某公園有三條觀光大道AB,BC,AC圍成直角三角形,其中直角邊BC=200m,斜邊AB=400m,現(xiàn)有甲、乙、丙三位小朋友分別在AB,BC,AC大道上嬉戲,所在位置分別記為點(diǎn)D,E,F(xiàn).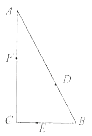
(1)若甲、乙都以每分鐘100m的速度從點(diǎn)B出發(fā)在各自的大道上奔走,到大道的另一端時(shí)即停,乙比甲遲2分鐘出發(fā),當(dāng)乙出發(fā)1分鐘后,求此時(shí)甲乙兩人之間的距離;
(2)設(shè)∠CEF=θ,乙丙之間的距離是甲乙之間距離的2倍,且∠DEF= ![]() ,請(qǐng)將甲乙之間的距離y表示為θ的函數(shù),并求甲乙之間的最小距離.
,請(qǐng)將甲乙之間的距離y表示為θ的函數(shù),并求甲乙之間的最小距離.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】近年來,“共享單車”的出現(xiàn)為市民“綠色出行”提供了極大的方便,某共享單車公司“Mobike”計(jì)劃在甲、乙兩座城市共投資120萬元,根據(jù)行業(yè)規(guī)定,每個(gè)城市至少要投資40萬元,由前期市場(chǎng)調(diào)研可知:甲城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,乙城市收益
,乙城市收益![]() 與投入
與投入![]() (單位:萬元)滿足
(單位:萬元)滿足![]() ,設(shè)甲城市的投入為
,設(shè)甲城市的投入為![]() (單位:萬元),兩個(gè)城市的總收益為
(單位:萬元),兩個(gè)城市的總收益為![]() (單位:萬元).
(單位:萬元).
(1)當(dāng)甲城市投資50萬元時(shí),求此時(shí)公司總收益;
(2)試問如何安排甲、乙兩個(gè)城市的投資,才能使總收益最大?
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖是由正整數(shù)構(gòu)成的數(shù)表,用![]() 表示第
表示第![]() 行第
行第![]() 個(gè)數(shù)(
個(gè)數(shù)(![]() ). 此表中
). 此表中![]() ,每行中除首尾兩數(shù)外,其他各數(shù)分別等于其“肩膀”上的兩數(shù)之和.
,每行中除首尾兩數(shù)外,其他各數(shù)分別等于其“肩膀”上的兩數(shù)之和.

(1)寫出數(shù)表的第6行(從左至右依次列出);
(2)設(shè)第![]() 行的第二個(gè)數(shù)為
行的第二個(gè)數(shù)為![]() ,求
,求![]() ;
;
(3)令![]() ,記
,記![]() 為數(shù)列
為數(shù)列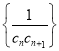 前
前![]() 項(xiàng)和,求
項(xiàng)和,求![]() 的最大值,并求此時(shí)
的最大值,并求此時(shí)![]() 的值.
的值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知數(shù)列{an}滿足:2a1+22a2+23a3+…+2nan=n(n∈N*),數(shù)列{ ![]() }的前n項(xiàng)和為Sn , 則S1S2S3…S10= .
}的前n項(xiàng)和為Sn , 則S1S2S3…S10= .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)z1 , z2是復(fù)數(shù),給出下列四個(gè)命題:
①若|z1﹣z2|=0,則 ![]() =
= ![]() ②若z1=
②若z1= ![]() ,則
,則 ![]() =z2
=z2
③若|z1|=|z2|,則z1 ![]() =z2
=z2 ![]() ④若|z1|=|z2|,則z12=z22
④若|z1|=|z2|,則z12=z22
其中真命題的序號(hào)是 .
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)平面向量基本定理,若![]() 為一組基底,同一平面的向量
為一組基底,同一平面的向量![]() 可以被唯一確定地表示為
可以被唯一確定地表示為 ![]() =
= ![]() ,則向量
,則向量![]() 與有序?qū)崝?shù)對(duì)
與有序?qū)崝?shù)對(duì)![]() 一一對(duì)應(yīng),稱
一一對(duì)應(yīng),稱![]() 為向量
為向量![]() 的基底
的基底![]() 下的坐標(biāo);特別地,若
下的坐標(biāo);特別地,若![]() 分別為
分別為![]() 軸正方向的單位向量
軸正方向的單位向量![]() ,則稱
,則稱![]() 為向量
為向量![]() 的直角坐標(biāo).
的直角坐標(biāo).
(I)據(jù)此證明向量加法的直角坐標(biāo)公式:若![]() ,則
,則![]() ;
;
(II)如圖,直角![]() 中,
中, ![]() ,
, ![]() 點(diǎn)在
點(diǎn)在![]() 上,且
上,且![]() ,求向量
,求向量![]() 在基底
在基底![]() 下的坐標(biāo).
下的坐標(biāo).

查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知直線  (
( ![]() 為參數(shù))以坐標(biāo)原點(diǎn)為極點(diǎn),
為參數(shù))以坐標(biāo)原點(diǎn)為極點(diǎn), ![]() 軸的正半軸為極軸建立極坐標(biāo)系,曲線
軸的正半軸為極軸建立極坐標(biāo)系,曲線 ![]() 的極坐標(biāo)方程為
的極坐標(biāo)方程為 ![]() .
.
(1)將曲線 ![]() 的極坐標(biāo)方程化為直角坐標(biāo)方程;
的極坐標(biāo)方程化為直角坐標(biāo)方程;
(2)設(shè)點(diǎn)M的直角坐標(biāo)為 ![]() ,直線l與曲線C的交點(diǎn)為A,B,求
,直線l與曲線C的交點(diǎn)為A,B,求 ![]() 的值.
的值.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com