求過直線x-2y+4=0與直線2x-y-1=0的交點,且與點A(0,4)和點B(4,O)距離相等的直線方程.
【答案】
分析:解方程組求得兩直線3x-y-10=0和x+y-2=0的交點M的坐標,直線l平行于AB時,用點斜式求直線方程.當直線l經(jīng)過AB的中點N(2,2)時,由MN垂直于x軸,可得.
解答:解:聯(lián)立方程
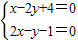
,解得
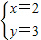
,
故兩直線x-2y+4=0和2x-y-1=0的交點M(2,3).
當所求直線l平行于AB時,斜率等于K
AB=
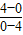
=-1,
故直線l的方程為 y-3=-(x-2),即 x+y-5=0.
當直線l經(jīng)過AB的中點N(2,2)時,
由于此時直線l經(jīng)過M、N兩點,且MN垂直于x軸,
故直線l的方程為 x=2.
綜上,所求直線l的方程為:x+y-5=0或x=2
點評:本題考查用點斜式求直線方程的方法,體現(xiàn)了分類討論的數(shù)學思想,注意考慮直線過AB的中點的情況,屬基礎題.

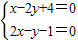 ,解得
,解得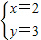 ,
,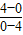 =-1,
=-1,

 閱讀快車系列答案
閱讀快車系列答案