【題目】雙曲線 
=1（a＞1，b＞0）的焦點距為2c，直線l過點（a，0）和（0，b），且點（1，0）到直線l的距離與點（﹣1，0）到直線l的距離之和 
．求雙曲線的離心率e的取值范圍．
科目：高中數學 來源： 題型：
【題目】若向量 
、 
、 
的起點與終點M、A、B、C互不重合且無三點共線，且滿足下列關系（O是空間任一點），則能使向量 、 、 成為空間一組基底的關系是（ ）
A.
B.
C.
D.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某校為了紀念“中國紅軍長征90周年”，增強學生對“長征精神”的深刻理解，在全校組織了一次有關“長征”的知識競賽，經過初賽、復賽，甲、乙兩個代表隊(每隊3人)進入了決賽，規定每人回答一個問題，答對為本隊贏得20分，答錯得0分.假設甲隊中每人答對的概率均為 
，乙隊中3人答對的概率分別為 
， ， 
，且各人回答正確與否相互之間沒有影響，用 
表示乙隊的總得分.
（1）求 的分布列和均值；
（2）求甲、乙兩隊總得分之和等于40分且甲隊獲勝的概率.
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知數據
是上海普通職工n
個人的年收入,設n個數據的中位數為x，平均數為y，方差為z，如果再加上世界首富的年收入
， 則這n+1個數據中，下列說法正確的是 ( )
A.年收入平均數大大增加，中位數一定變大，方差可能不變
B.年收入平均數大大增加，中位數可能不變，方差變大
C.年收入平均數大大增加，中位數可能不變，方差也不變
D.年收入平均數可能不變，中位數可能不變，方差可能不變
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】我國是世界上嚴重缺水的國家，某市政府為了鼓勵居民節約用水，計劃調整居民生活用水收費方案，擬確定一個合理的月用水量標準x（噸），一位居民的月用水量不超過x的部分按平價收費，超出x的部分按議價收費．為了了解居民用水情況，通過抽樣，獲得了某年100位居民每人的月均用水量（單位：噸），將數據按照[0，0.5），[0.5，1），…，[4，4.5）分成9組，制成了如圖所示的頻率分布直方圖．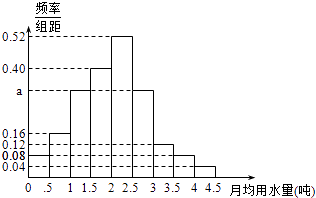 
（Ⅰ）求直方圖中a的值；
（Ⅱ）設該市有30萬居民，估計全市居民中月均用水量不低于3噸的人數，并說明理由；
（Ⅲ）若該市政府希望使85%的居民每月的用水量不超過標準x（噸），估計x的值，并說明理由．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】十八屆五中全會公報指出：努力促進人口均衡發展，堅持計劃生育的基本國策，完善人口發展戰略，全面實施一對夫婦可生育兩個孩子的政策，提高生殖健康、婦幼保健、托幼等公共服務水平．為了解適齡公務員對放開生育二胎政策的態度，某部門隨機調查了100位30到40歲的公務員，得到情況如下表：
男公務員 | 女公務員 | |
生二胎 | 40 | 20 |
不生二胎 | 20 | 20 |
（1）是否有95%以上的把握認為“生二胎與性別有關”，并說明理由；
（2）把以上頻率當概率，若從社會上隨機抽取3位30到40歲的男公務員，記其中生二胎的人數為X，求隨機變量X的分布列，數學期望．
附：K2= 
P（K2≥k0） | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】已知等差數列{an}的前n項和為Sn ， 且a3=3，S7=28，在等比數列{bn}中，b3=4，b4=8．
（1）求an及bn；
（2）設數列{anbn}的前n項和為Tn ， 求Tn ．
查看答案和解析>>
科目：高中數學 來源： 題型：
【題目】某班級50名學生的考試分數x分布在區間[50，100）內，設分數x的分布頻率是f（x）且f（x）=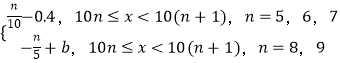 
，考試成績采用“5分制”，規定：考試分數在[50，60）內的成績記為1分，考試分數在[60，70）內的成績記為2分，考試分數在[70，80）內的成績記為3分，考試分數在[80，90）內的成績記為4分，考試分數在[90，100）內的成績記為5分．用分層抽樣的方法，現在從成績在1分，2分及3分的人中用分層抽樣隨機抽出6人，再從這6人中抽出3人，記這3人的成績之和為ξ（將頻率視為概率）．
（1）求b的值，并估計班級的考試平均分數；
（2）求P（ξ=7）；
（3）求ξ的分布列和數學期望．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
