
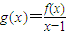 .
.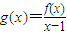 =
=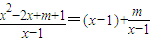 .利用導數研究其單調性,從而得出極值的情形;
.利用導數研究其單調性,從而得出極值的情形;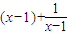 .利用二項定理化簡式子[g(x+1)]n-g(xn+1),再利用組合數的性質或數學歸納法進行證明即得對?n∈N*,[g(x+1)]n-g(xn+1)≥2n-2都成立.
.利用二項定理化簡式子[g(x+1)]n-g(xn+1),再利用組合數的性質或數學歸納法進行證明即得對?n∈N*,[g(x+1)]n-g(xn+1)≥2n-2都成立.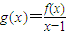 =
=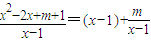 .
.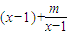 -kln(x-1)的定義域為(1,+∞).
-kln(x-1)的定義域為(1,+∞).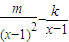 =
=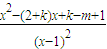 .…(3分)
.…(3分)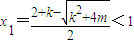 ,
,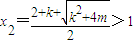 ,…(5分)
,…(5分)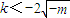 或
或 ,
,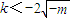 ,則
,則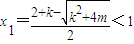 ,
,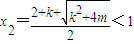 ,
,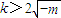 時,
時,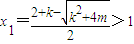 ,
,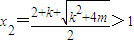 ,
, ,函數φ(x)有極小值點x2,有極大值點x1.…(9分)
,函數φ(x)有極小值點x2,有極大值點x1.…(9分)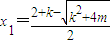 ,
,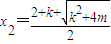 )
)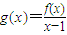 =
=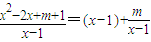 .
.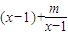 -kln(x-1)的定義域為(1,+∞).
-kln(x-1)的定義域為(1,+∞).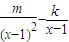 =
=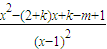 .…(3分)
.…(3分)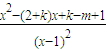 =0,
=0,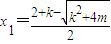 ,
,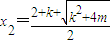 .
.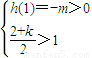 得
得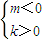
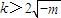 或
或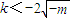 ,
,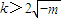 .…(7分)
.…(7分)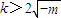 ,函數φ(x)有極小值點x2,有極大值點x1.…(9分)
,函數φ(x)有極小值點x2,有極大值點x1.…(9分)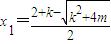 ,
,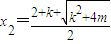 )
)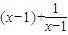 .
.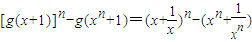 =
=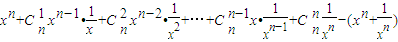
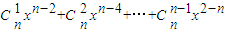 .…(10分)
.…(10分)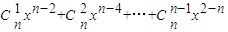 ,
,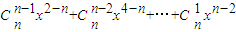 =
=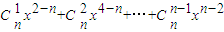 .
. …(11分)≥
…(11分)≥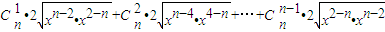 …(12分)
…(12分)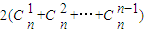 =
=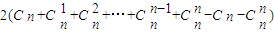 =2(2n-2).…(13分)
=2(2n-2).…(13分)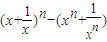 ≥2n-2.
≥2n-2.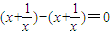 ,右邊=21-2=0,不等式成立;
,右邊=21-2=0,不等式成立;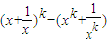 ≥2k-2,
≥2k-2,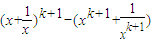 =
=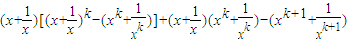 =
=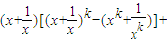
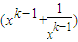 …(11分)
…(11分)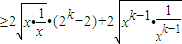 =2k+1-2.…(13分)
=2k+1-2.…(13分)

 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| f(x) | x-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com