
 lgx,將其代入到f(x)=(lgx)2+(lgy)2中即可得到(lgx)2+(lgy)2關于lgx的一元二次函數,令lgx=t,換元后由二次函數的性質求最值,及相應的x,y的值
lgx,將其代入到f(x)=(lgx)2+(lgy)2中即可得到(lgx)2+(lgy)2關于lgx的一元二次函數,令lgx=t,換元后由二次函數的性質求最值,及相應的x,y的值 lgx.f(x)=(lgx)2+(lgy)2=(lgx)2+[1-
lgx.f(x)=(lgx)2+(lgy)2=(lgx)2+[1- lgx]2=
lgx]2= (lgx)2-lgx+1 設lgx=t,則有0≤t≤1,f(x)=
(lgx)2-lgx+1 設lgx=t,則有0≤t≤1,f(x)= t2-t+1 對稱軸t=
t2-t+1 對稱軸t= ,在區間[0,1]范圍內,所以:f(x)在t=
,在區間[0,1]范圍內,所以:f(x)在t= 處取得最小值,此時x=
處取得最小值,此時x=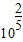 ,y=
,y=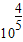 ; f(x)在t=1處取得最大值,此時x=10,y=
; f(x)在t=1處取得最大值,此時x=10,y=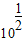 .
.

湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com