設F為拋物線C:y2=2px(p>0)的焦點,過F且與拋物線C對稱軸垂直的直線被拋物線C截得線段長為4.
(1)求拋物線C方程.
(2)設A、B為拋物線C上異于原點的兩點且滿足FA⊥FB,延長AF、BF分別拋物線C于點C、D.求:四邊形ABCD面積的最小值.
【答案】
分析:(1)根據過F且與拋物線C對稱軸垂直的直線被拋物線C截得線段長為4,可得2p=8,從而可得拋物線C的方程;
(2)設出直線方程與拋物線方程聯立,計算出|AC|、|BD|,可得S=

|AC||BD|=8(
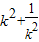
+2),利用基本不等式,即可求四邊形ABCD面積的最小值.
解答:解:(1)由條件得2p=4,∴拋物線C的方程為y
2=4x;
(2)兩直線垂直,焦點為(1,0),不妨設兩直線為:y=k(x-1)(k≠0)與ky=1-x
y=k(x-1)與拋物線方程聯立,可得k
2 x
2-2(k
2+2)x+k
2=0,
設A(x
1,y
1),C(x
2,y
2),則|x
1-x
2|=
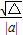
=
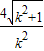
∴弦長|AC|=
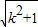
|x
1-x
2|=
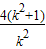
同理可得,弦長|BD|=4(k
2+1)
∵兩條直線相互垂直,∴這個四邊形的面積S=

|AC||BD|=8(
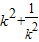
+2)≥8(2
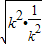
+2)=32
當且僅當k=±1時等號成立,此時取到面積最小值為32.
點評:本題考查拋物線的標準方程,考查直線與拋物線的位置關系,考查四邊形面積的計算,考查基本不等式的運用,屬于中檔題.

 |AC||BD|=8(
|AC||BD|=8(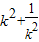 +2),利用基本不等式,即可求四邊形ABCD面積的最小值.
+2),利用基本不等式,即可求四邊形ABCD面積的最小值.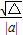 =
=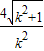
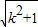 |x1-x2|=
|x1-x2|=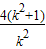
 |AC||BD|=8(
|AC||BD|=8(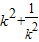 +2)≥8(2
+2)≥8(2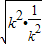 +2)=32
+2)=32
