
已知![]() ,
,![]() ,規定:當
,規定:當![]() 時,
時, ![]() ;當
;當![]() 時,
時, ![]() ,則
,則![]()
A. 有最小值![]() ,最大值1 B. 有最大值1,無最小值
,最大值1 B. 有最大值1,無最小值
C. 有最小值![]() ,無最大值 D. 有最大值
,無最大值 D. 有最大值![]() ,無最小值
,無最小值

 培優好卷單元加期末卷系列答案
培優好卷單元加期末卷系列答案科目:高中數學 來源: 題型:
如圖,已知圓![]() 與
與![]() 軸負半軸的交點為
軸負半軸的交點為![]() . 由點
. 由點![]() 出發的射線
出發的射線![]() 的斜率為
的斜率為![]() . 射線
. 射線![]() 與圓
與圓![]() 相交于另一點
相交于另一點![]()

(1)當![]() 時,試用
時,試用![]() 表示點
表示點![]() 的坐標;
的坐標;
(2)當![]() 時,求證:“射線
時,求證:“射線![]() 的斜率
的斜率![]() 為有理數”是“點
為有理數”是“點![]() 為單位圓
為單位圓![]() 上的有理點”的充要條件;(說明:坐標平面上,橫、縱坐標都為有理數的點為有理點.我們知道,一個有理數可以表示為
上的有理點”的充要條件;(說明:坐標平面上,橫、縱坐標都為有理數的點為有理點.我們知道,一個有理數可以表示為![]() ,其中
,其中![]() 、
、![]() 均為整數且
均為整數且![]() 、
、![]() 互質)
互質)
(3)定義:實半軸長![]() 、虛半軸長
、虛半軸長![]() 和半焦距
和半焦距![]() 都是正整數的雙曲線為“整勾股雙曲線”.
都是正整數的雙曲線為“整勾股雙曲線”.
當![]() 為有理數且
為有理數且![]() 時,試證明:一定能構造偶數個“整勾股雙曲線”(規定:實軸長和虛軸長都對應相等的雙曲線為同一個雙曲線),它的實半軸長、虛半軸長和半焦距的長恰可由點
時,試證明:一定能構造偶數個“整勾股雙曲線”(規定:實軸長和虛軸長都對應相等的雙曲線為同一個雙曲線),它的實半軸長、虛半軸長和半焦距的長恰可由點![]() 的橫坐標、縱坐標和半徑
的橫坐標、縱坐標和半徑![]() 的數值構成. 說明你的理由并請嘗試給出構造方法.
的數值構成. 說明你的理由并請嘗試給出構造方法.
查看答案和解析>>
科目:高中數學 來源:2013-2014學年河北唐山一中高三下學期調研考試理科數學試卷(解析版) 題型:選擇題
已知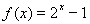 ,
, ,規定:當
,規定:當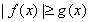 時,
時, 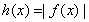 ;當
;當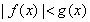 時,
時,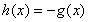 ,則
,則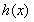 ( )
( )
A.有最小值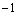 ,最大值1 B.有最大值1,無最小值
,最大值1 B.有最大值1,無最小值
C.有最小值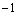 ,無最大值 D.有最大值
,無最大值 D.有最大值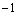 ,無最小值
,無最小值
查看答案和解析>>
科目:高中數學 來源:2011-2012學年湖南省、岳陽縣一中高三11月聯考文科數學 題型:填空題
已知集合 為非空集合,且
為非空集合,且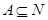 ,定義
,定義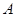 的“交替和”如下:將集合
的“交替和”如下:將集合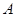 中的元素按由大到小排列,然后從最大的數開始,交替地減、加后續的數,直到最后一個數,并規定單元素集合的交替和為該元素。例如集合
中的元素按由大到小排列,然后從最大的數開始,交替地減、加后續的數,直到最后一個數,并規定單元素集合的交替和為該元素。例如集合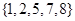 的交替和為8-7+5-2+1=5,集合
的交替和為8-7+5-2+1=5,集合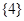 的交替和為4,當
的交替和為4,當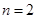 時,集合
時,集合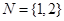 的非空子集為
的非空子集為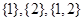 ,記三個集合的交替和的總和為
,記三個集合的交替和的總和為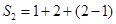 = 4,則
= 4,則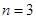 時,集合
時,集合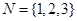 的所有非空子集的交替和的總和
的所有非空子集的交替和的總和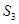 =
;集合
=
;集合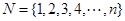 的所有非空子集的交替和的總和
的所有非空子集的交替和的總和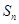 =
=
查看答案和解析>>
科目:高中數學 來源:2010-2011學年福建省高三上學期期末考試數學文卷 題型:解答題
(14分)已知函數 ,
,
(Ⅰ)若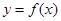 在[-1,1]上存在零點,求實數
在[-1,1]上存在零點,求實數 的取值范圍;
的取值范圍;
(Ⅱ)當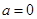 時,若對任意的
時,若對任意的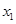 ∈[1,4],總存在
∈[1,4],總存在 ∈[1,4],使
∈[1,4],使 成立,求實數
成立,求實數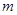 的取值范圍;
的取值范圍;
(Ⅲ)若函數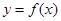 (其中
(其中 )的值域為區間D,是否存在常數
)的值域為區間D,是否存在常數 ,使區間D的長度為
,使區間D的長度為 ?若存在,求出
?若存在,求出 的值;若不存在,請說明理由。(規定:區間
的值;若不存在,請說明理由。(規定:區間 的長度為
的長度為 ).
).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com