
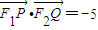 .
.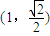 .
.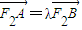 ,若
,若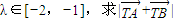 的取值范圍.
的取值范圍.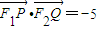 進行求解;
進行求解;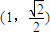 ,結合a2=b2+1 即可求得a2,b2的值,則橢圓方程可求;
,結合a2=b2+1 即可求得a2,b2的值,則橢圓方程可求;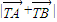 的值,當直線斜率存在時,設出直線方程,和橢圓方程聯立后,利用
的值,當直線斜率存在時,設出直線方程,和橢圓方程聯立后,利用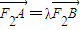 ,消掉點的坐標得到λ與k的關系,根據λ的范圍求k的范圍,然后把
,消掉點的坐標得到λ與k的關系,根據λ的范圍求k的范圍,然后把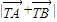 轉化為含有k的函數式,最后利用基本不等式求出
轉化為含有k的函數式,最后利用基本不等式求出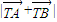 的取值范圍.
的取值范圍.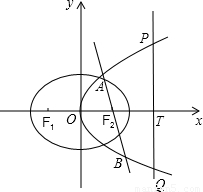
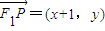 ,
,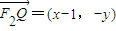 .
.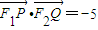 ,
,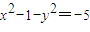 ,即
,即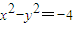 ①
①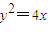 ②
②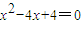 ,解得:x=2.
,解得:x=2.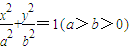 ,
,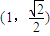 ,
,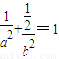 ③
③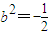 (舍去)
(舍去)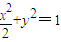 .
.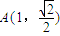 ,
,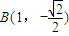 ,
,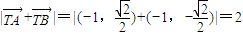 ;
;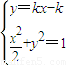 ,得(1+2k2)x2-4k2x+2k2-2=0
,得(1+2k2)x2-4k2x+2k2-2=0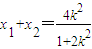 ,
,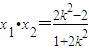 .
.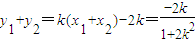 ⑤
⑤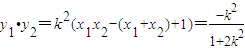 ⑥
⑥ ,所以
,所以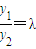 ,且λ<0.
,且λ<0.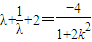
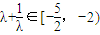 ,即
,即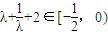 .
.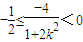 ,解得
,解得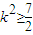 .
.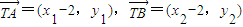 ,所以
,所以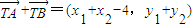 ,
,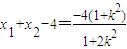 ,
,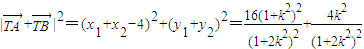
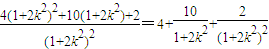 .
.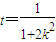 ,因為
,因為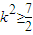 ,所以
,所以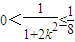 ,即
,即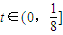 ,
,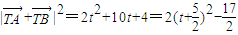
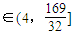 .
.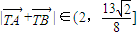
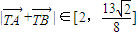 .
.

科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| y | 2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 已知拋物線y2=4x,焦點為F,頂點為O,點P(m,n)在拋物線上移動,Q是OP的中點,M是FQ的中點.
已知拋物線y2=4x,焦點為F,頂點為O,點P(m,n)在拋物線上移動,Q是OP的中點,M是FQ的中點.| n | m+3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com