
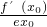 =
= (t-1)2,并確定這樣的x0的個數.
(t-1)2,并確定這樣的x0的個數. <e,
<e,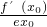 =x2-x0,所以
=x2-x0,所以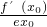 =
= (t-1)2,即為x2-x0=
(t-1)2,即為x2-x0= (t-1)2.
(t-1)2. (t-1)2,從而問題轉化為證明方程g(x)=x2-x-
(t-1)2,從而問題轉化為證明方程g(x)=x2-x- (t-1)2=0
(t-1)2=0 (t-1)2=-
(t-1)2=- (t+2)(t-4),g(t)=t(t-1)-
(t+2)(t-4),g(t)=t(t-1)- (t-1)2=
(t-1)2= (t+2)(t-1),
(t+2)(t-1), (t-1)2<0,
(t-1)2<0,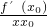 =
= (t-1)2,
(t-1)2,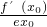 =x2-x0,然后轉化成方程x2-x-
=x2-x0,然后轉化成方程x2-x- (t-1)2=0在(-2,t)上有解的問題,分類討論確定x0的個數.
(t-1)2=0在(-2,t)上有解的問題,分類討論確定x0的個數.

 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•x2 |
| 1+m•x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2 |
| 1 |
| 4 |
| 1-m•x2 |
| 1+m•x2 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| x |
| x2-1 |
查看答案和解析>>
科目:高中數學 來源: 題型:
 如右圖所示,定義在D上的函數f(x),如果滿足:對?x∈D,常數A,都有f(x)≥A成立,則稱函數f(x)在D上有下界,其中A稱為函數的下界.(提示:圖中的常數A可以是正數,也可以是負數或零)
如右圖所示,定義在D上的函數f(x),如果滿足:對?x∈D,常數A,都有f(x)≥A成立,則稱函數f(x)在D上有下界,其中A稱為函數的下界.(提示:圖中的常數A可以是正數,也可以是負數或零)| 48 |
| x |
| t+1 |
| 1 |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com