
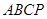 中,
中,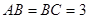 ,
,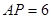 ,
,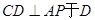 ,現(xiàn)將
,現(xiàn)將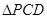 沿線段
沿線段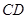 折成
折成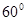 的二面角
的二面角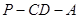 ,設
,設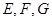 分別是
分別是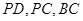 的中點.
的中點.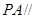 平面
平面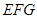 ;
;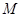 為線段
為線段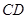 上的動點,問點
上的動點,問點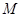 在什么位置時,
在什么位置時,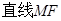 與平面
與平面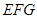 所成角為
所成角為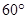 .
.
 王后雄學案教材完全解讀系列答案
王后雄學案教材完全解讀系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
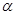 是空間中的一個平面,
是空間中的一個平面,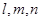 是三條不同的直線,
是三條不同的直線, 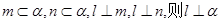 ; ②若
; ②若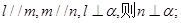
 ,則
,則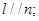 ④若
④若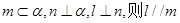 ;
;| A.①② | B.②③ | C.③④ | D.①④ |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:填空題
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
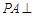 矩形
矩形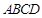 所在平面,
所在平面,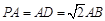 ,
,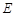 為線段
為線段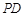 上一點,
上一點,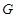 為線段
為線段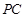
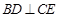 ;
;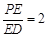 時,求證:BG//平面AEC.
時,求證:BG//平面AEC.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
 中(圖1),
中(圖1), 是
是 的中點,
的中點, ,
,
 ,
, 將(圖1)沿直線
將(圖1)沿直線 折起,使二面角
折起,使二面角 為
為 (如圖2)
(如圖2) 平面
平面 ;
; 與
與 所成角的余弦值;
所成角的余弦值; 到平面
到平面 的距離.
的距離.
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:解答題
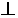 平面ABCD,
平面ABCD,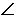 ABC=60O,E,F(xiàn)分別是BC,PC
ABC=60O,E,F(xiàn)分別是BC,PC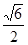 。
。 PD;
PD;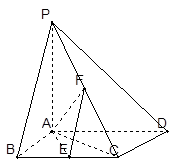
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com