
若圓x2+y2=4上每個點的橫坐標不變.縱坐標縮短為原來的 ,則所得曲線的方程是( )
,則所得曲線的方程是( )
A.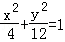 B.
B.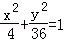 C.
C.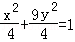 D.
D.
 全能練考卷系列答案
全能練考卷系列答案科目:高中數學 來源:[同步]2014年新人教A版選修4-2 2.1復合變換與二階矩陣的乘法(解析版) 題型:填空題
(矩陣與變換)已知矩陣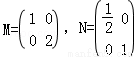 ,矩陣MN對應的變換把曲線y=sinx變為曲線C,求C的方程.
,矩陣MN對應的變換把曲線y=sinx變為曲線C,求C的方程.
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-2 1.1線性變換與二階矩陣練習卷(解析版) 題型:填空題
在同一坐標系中,將曲線y=2sin3x變為曲線y=sinx的伸縮變換是
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-2 1.1線性變換與二階矩陣練習卷(解析版) 題型:選擇題
已知函數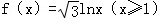 ,若將其圖象繞原點逆時針旋轉
,若將其圖象繞原點逆時針旋轉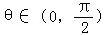 角后,所得圖象仍是某函數的圖象,則當角θ取最大值θ0時,tanθ0=( )
角后,所得圖象仍是某函數的圖象,則當角θ取最大值θ0時,tanθ0=( )
A.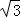 B.
B. C.
C.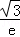 D.
D.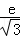
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-2 1.1線性變換與二階矩陣練習卷(解析版) 題型:選擇題
正弦曲線y=sinx通過坐標變換公式 ,變換得到的新曲線為( )
,變換得到的新曲線為( )
A.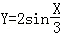 B.Y=2sin3X C.
B.Y=2sin3X C.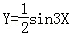 D.
D.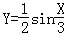
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-1 3.3平面與圓錐面的截線練習卷(解析版) 題型:解答題
(2010•順義區一模)已知橢圓C: ,(a>b>0)的兩焦點分別為F1、F2,
,(a>b>0)的兩焦點分別為F1、F2, ,離心率
,離心率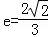 .過直線l:
.過直線l: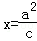 上任意一點M,引橢圓C的兩條切線,切點為A、B.
上任意一點M,引橢圓C的兩條切線,切點為A、B.
(1)在圓中有如下結論:“過圓x2+y2=r2上一點P(x0,y0)處的切線方程為:x0x+y0y=r2”.由上述結論類比得到:“過橢圓 (a>b>0),上一點P(x0,y0)處的切線方程”(只寫類比結論,不必證明).
(a>b>0),上一點P(x0,y0)處的切線方程”(只寫類比結論,不必證明).
(2)利用(1)中的結論證明直線AB恒過定點( );
);
(3)當點M的縱坐標為1時,求△ABM的面積.
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-1 3.1平行射影練習卷(解析版) 題型:填空題
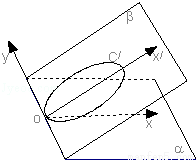
如圖,直角坐標系x'oy所在的平面為β,直角坐標系xoy所在的平面為α,且二面角α﹣y軸﹣β的大小等于30°.已知β內的曲線C'的方程是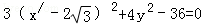 ,則曲線C'在α內的射影的曲線方程是 .
,則曲線C'在α內的射影的曲線方程是 .
查看答案和解析>>
科目:高中數學 來源:[同步]2014年新人教A版選修4-1 2.1圓周角定理練習卷(解析版) 題型:填空題
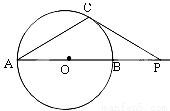
(2012•惠州一模)如圖,AB是⊙O的直徑,P是AB延長線上的一點.過P作⊙O的切線,切點為C,PC=2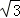 ,若∠CAP=30°,則⊙O的直徑AB= .
,若∠CAP=30°,則⊙O的直徑AB= .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com