
【題目】對于函數![]() 定義
定義![]() 已知偶函數
已知偶函數![]() 的定義域為
的定義域為![]() 當
當![]() 且
且![]() 時,
時,![]()
(1)求![]() 并求出函數
并求出函數![]() 的解析式;
的解析式;
(2)若存在實數![]() 使得函數
使得函數![]() 在
在![]() 上的值域為
上的值域為![]() ,求實數
,求實數![]() 的取值范圍.
的取值范圍.
【答案】(1)![]()
![]() ,
,![]() ,
,![]() (2)
(2)![]()
【解析】
(1)按![]() 的規律,逐步計算
的規律,逐步計算![]() 觀察發現對任意的
觀察發現對任意的![]() ,有
,有![]() 從而求出
從而求出![]() ,由
,由![]() 是偶函數可求得函數
是偶函數可求得函數![]() 的解析式;
的解析式;
(2)由題意可知![]() 在
在![]() 上遞減且
上遞減且![]() ,分
,分![]() 和
和![]() 兩種情況討論,在
兩種情況討論,在![]() 時得出
時得出![]() 推出矛盾,在
推出矛盾,在![]() 時可將問題轉化為
時可將問題轉化為![]() 是方程
是方程![]() 的兩個不相等的負實數根,轉化為一元二次方程
的兩個不相等的負實數根,轉化為一元二次方程![]() 有兩個不相等的負根,由根與系數的關系列出不等式組求出
有兩個不相等的負根,由根與系數的關系列出不等式組求出![]() 的取值范圍
的取值范圍
(1)因為![]()
故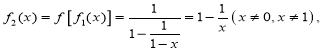
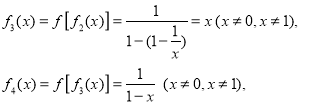
故對任意的![]() ,有
,有![]()
于是![]()
故當![]() 時,
時,![]()
又![]() ,故當
,故當![]() 時,
時,![]()
由![]() 為偶函數,當
為偶函數,當![]() 時,
時,![]()
因此,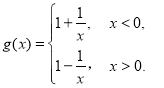 ,即
,即![]() ;
;
(2)由于![]() 的定義域為
的定義域為![]() ,
,
又![]() 可知
可知![]() 與b同號,且
與b同號,且![]() ,
,
函數![]() 的圖象,如圖所示
的圖象,如圖所示
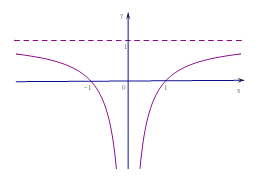
若![]() ,則
,則![]() 在
在![]() 上單調遞增,有
上單調遞增,有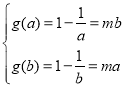 ,
,![]()
所以![]() ,解得
,解得![]() ,不符合題意,舍去;
,不符合題意,舍去;
若![]() ,則
,則![]() 在
在![]() 上單調遞減,由題意,有
上單調遞減,由題意,有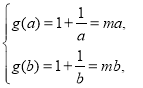
故![]() 是方程
是方程![]() 的兩個不相等的負實數根,即方程
的兩個不相等的負實數根,即方程![]() 在
在![]() 上有
上有
兩個不相等的實根,于是
綜合上述,實數![]() 的取值范圍為
的取值范圍為![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】當前,以“立德樹人”為目標的課程改革正在有序推進.高中聯招對初三畢業學生進行體育測試,是激發學生、家長和學校積極開展體育活動,保證學生健康成長的有效措施.某地區2019年初中畢業生升學體育考試規定,考生必須參加立定跳遠、擲實心球、1分鐘跳繩三項測試,三項考試滿分為50分,其中立定跳遠15分,擲實心球15分,1分鐘跳繩20分.某學校在初三上期開始時要掌握全年級學生每分鐘跳繩的情況,隨機抽取了100名學生進行測試,得到如下頻率分布直方圖,且規定計分規則如下表:
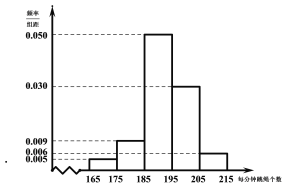
每分鐘跳 繩個數 |
|
|
|
|
|
得分 | 16 | 17 | 18 | 19 | 20 |
(Ⅰ)現從樣本的100名學生中,任意選取2人,求兩人得分之和不大于33分的概率;
(Ⅱ)若該校初三年級所有學生的跳繩個數![]() 服從正態分布
服從正態分布![]() ,用樣本數據的平均值和方差估計總體的期望和方差(結果四舍五入到整數),已知樣本方差
,用樣本數據的平均值和方差估計總體的期望和方差(結果四舍五入到整數),已知樣本方差![]() (各組數據用中點值代替).根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步,假設明年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,利用現所得正態分布模型:
(各組數據用中點值代替).根據往年經驗,該校初三年級學生經過一年的訓練,正式測試時每人每分鐘跳繩個數都有明顯進步,假設明年正式測試時每人每分鐘跳繩個數比初三上學期開始時個數增加10個,利用現所得正態分布模型:
(ⅰ)預估全年級恰好有1000名學生,正式測試時每分鐘跳193個以上的人數.(結果四舍五入到整數)
(ⅱ)若在該地區2020年所有初三畢業生中任意選取3人,記正式測試時每分鐘跳202個以上的人數為![]() ,求隨機變量
,求隨機變量![]() 的分布列和期望.
的分布列和期望.
附:若隨機變量![]() 服從正態分布
服從正態分布![]() ,
,![]() ,則
,則![]() ,
,
![]() ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】數列![]() 滿足
滿足![]() .
.
①存在![]() 可以生成的數列
可以生成的數列![]() 是常數數列;
是常數數列;
②“數列![]() 中存在某一項
中存在某一項![]() ”是“數列
”是“數列![]() 為有窮數列”的充要條件;
為有窮數列”的充要條件;
③若![]() 為單調遞增數列,則
為單調遞增數列,則![]() 的取值范圍是
的取值范圍是![]() ;
;
④只要![]() ,其中
,其中![]() ,則
,則![]() 一定存在;
一定存在;
其中正確命題的序號為__________.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的焦點為橢圓
的焦點為橢圓![]() 的右焦點,且橢圓長軸的長為4,
的右焦點,且橢圓長軸的長為4,![]() 、
、![]() 是橢圓上的兩點;
是橢圓上的兩點;
(1)求橢圓標準方程;
(2)若直線![]() 經過點
經過點![]() ,且
,且![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)若動點![]() 滿足:
滿足:![]() ,直線
,直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,是否存在兩個定點
,是否存在兩個定點![]() 、
、![]() ,使得
,使得![]() 為定值?若存在,求出
為定值?若存在,求出![]() 、
、![]() 的坐標;若不存在,請說明理由;
的坐標;若不存在,請說明理由;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《算法統宗》全稱《新編直指算法統宗》,是屮國古代數學名著,程大位著.書中有如下問題:“今有五人均銀四十兩,甲得十兩四錢,戊得五兩六錢.問:次第均之,乙丙丁各該若干?”意思是:有5人分40兩銀子,甲分10兩4錢,戊分5兩6錢,且相鄰兩項差相等,則乙丙丁各分幾兩幾錢?(注:1兩等于10錢)( )
A.乙分8兩,丙分8兩,丁分8兩B.乙分8兩2錢,丙分8兩,丁分7兩8錢
C.乙分9兩2錢,丙分8兩,丁分6兩8錢D.乙分9兩,丙分8兩,丁分7兩
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知數列![]() 是公差
是公差![]() 的等差數列,且
的等差數列,且![]() .
.
(1)求![]() 的前
的前![]() 項的和
項的和![]() ;
;
(2)若![]() ,問在數列
,問在數列![]() 中是否存在一項
中是否存在一項![]() (
(![]() 是正整數),使得
是正整數),使得![]() 成等比數列,若存在,求出
成等比數列,若存在,求出![]() 的值,若不存在,請說明理由;
的值,若不存在,請說明理由;
(3)若存在自然數![]() (
(![]() 是正整數),滿足
是正整數),滿足![]() ,使得
,使得![]() 成等比數列,求所有整數
成等比數列,求所有整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設數列![]() 滿足
滿足![]() ,其中A,B是兩個確定的實數,
,其中A,B是兩個確定的實數,![]()
(1)若![]() ,求
,求![]() 的前n項和;
的前n項和;
(2)證明:![]() 不是等比數列;
不是等比數列;
(3)若![]() ,數列
,數列![]() 中除去開始的兩項外,是否還有相等的兩項,并證明你的結論.
中除去開始的兩項外,是否還有相等的兩項,并證明你的結論.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】現有流量均為![]() 的兩條河流
的兩條河流![]() 匯合于某處后,不斷混合,它們的含沙量分別為
匯合于某處后,不斷混合,它們的含沙量分別為![]() 和
和![]() .假設從匯合處開始,沿岸設有若干個觀測點,兩股水流在流往相鄰兩個觀測點的過程中,其混合效果相當于兩股水流在1秒內交換
.假設從匯合處開始,沿岸設有若干個觀測點,兩股水流在流往相鄰兩個觀測點的過程中,其混合效果相當于兩股水流在1秒內交換![]() 的水量,其交換過程為從A股流入B股
的水量,其交換過程為從A股流入B股![]() 的水量,經混合后,又從B股流入A股
的水量,經混合后,又從B股流入A股![]() 水并混合,問從第幾個觀測點開始,兩股河水的含沙量之差小于
水并混合,問從第幾個觀測點開始,兩股河水的含沙量之差小于![]() .(不考慮泥沙沉淀).
.(不考慮泥沙沉淀).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,三棱錐![]() ,側棱
,側棱![]() ,底面三角形
,底面三角形![]() 為正三角形,邊長為
為正三角形,邊長為![]() ,頂點
,頂點![]() 在平面
在平面![]() 上的射影為
上的射影為![]() ,有
,有![]() ,且
,且![]() .
.
(Ⅰ)求證: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值;
的余弦值;
(Ⅲ)線段![]() 上是否存在點
上是否存在點![]() 使得
使得![]() ⊥平面
⊥平面![]() ,如果存在,求
,如果存在,求![]() 的值;如果不存在,請說明理由.
的值;如果不存在,請說明理由.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com