Question

在平面直角坐標(biāo)系中,已知矩形ABCD的長(zhǎng)為2,寬為1,AB、AD邊分別在x軸、y軸的正半軸上,A點(diǎn)與坐標(biāo)原點(diǎn)重合(如下圖所示).將矩形折疊,使A點(diǎn)落在線段DC上.

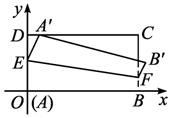
(1)若折痕所在直線的斜率為k,試寫出折痕所在直線的方程;

(2)求折痕的長(zhǎng)的最大值.

Answer 1

解:(1)設(shè)折疊后A在DC邊上對(duì)應(yīng)的點(diǎn)為A′,則折痕EF所在直線的斜率k≤0.

    當(dāng)k=0時(shí),A′與D重合,EF所在直線方程為y=.

    當(dāng)k＜0時(shí),EF垂直平分OA′.

    故直線OA′的方程為y=-x,則當(dāng)A′與C重合時(shí)k=-2.

    設(shè)OA′交EF于G點(diǎn),則G點(diǎn)坐標(biāo)為(-,),得EF所在直線的方程為y=kx+.

(2)由(1)得線段EF的方程為y=kx+(-2≤k≤0).                  (*)

    當(dāng)E與D重合時(shí),E點(diǎn)坐標(biāo)為(0,1),由(*)式得k=-1.

    當(dāng)F與B重合時(shí),F點(diǎn)坐標(biāo)為(2,0),由(*)式得k=-2+.

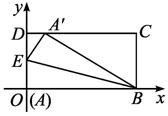
    ①當(dāng)-2+≤k≤0時(shí),E在OD上,F在BC上.

    由(*)式得E(0,)、F(2,).

    令l=|EF|²,則l=4k²+4(-2+≤k≤0)是k的減函數(shù).

    此時(shí)l≤l(-2+)=32-16.

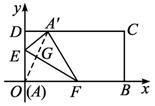
②當(dāng)-1≤k≤-2+時(shí),E在OD上,F在OB上.

    于是由(*)式得E(0,)、F(-,0).

    則l=|EF|²=()²+()²=.l_k′=.

    令l_k′=02k²-1=0k=-.

    當(dāng)-1≤k＜-時(shí),l_k′＜0,則l是k的減函數(shù).

    此時(shí)l≤l(-1)=2.

    當(dāng)-＜k≤-2+時(shí),l_k′＞0,則l是k的增函數(shù).

    此時(shí)l≤l(-2+)=32-16.(可由①直接得到)

③當(dāng)-2≤k≤-1時(shí),E在DC上,F在OB上.

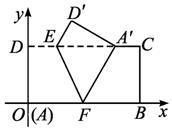
    由(*)式得E(,1)、F(-,0),

    則l=|EF|²=+1(-2≤k≤-1)是k的增函數(shù).

    此時(shí)l≤l(-1)=2.(可由②直接得到)

    綜上所述,l=|EF|²的最大值為l(-1)和l(-2+)中的最大者.

    因32-16=16(2-)＞16(2-1.75)=4,故l=32-16.

    所以折痕EF的最大值為.