
已知函數f(x)=3x+k(k為常數),A(-2k,2)是函數y= f -1(x)圖象上的點.
(1)求實數k的值及函數f -1(x)的解析式;
(2)將y= f -1(x)的圖象按向量a=(3,0)平移,得到函數y=g(x)的圖象,若2 f -1(x+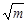 -3)-g(x)≥1恒成立,試求實數m的取值范圍.
-3)-g(x)≥1恒成立,試求實數m的取值范圍.
(1)f -1(x)=log3(x+3)(x>-3).(2)m≥ .
.
【解析】主要考查指數函數、對數函數互為反函數關系、反函數概念及反函數求法。
解:(1)∵A(-2k,2)是函數y= f -1(x)圖象上的點,
∴B(2,-2k)是函數y=f(x)上的點.
∴-2k=32+k.∴k=-3.
∴f(x)=3x-3.
∴y= f -1(x)=log3(x+3)(x>-3).
(2)將y= f -1(x)的圖象按向量a=(3,0)平移,得到函數y=g(x)=log3x(x>0),要使2 f -1(x+ -3)-g(x)≥1恒成立,即使2log3(x+
-3)-g(x)≥1恒成立,即使2log3(x+ )-log3x≥1恒成立,所以有x+
)-log3x≥1恒成立,所以有x+ +2
+2 ≥3在x>0時恒成立,只要(x+
≥3在x>0時恒成立,只要(x+ +2
+2 )min≥3.
)min≥3.
又x+ ≥2
≥2 (當且僅當x=
(當且僅當x= ,即x=
,即x= 時等號成立),∴(x+
時等號成立),∴(x+ +2
+2 )min=4
)min=4 ,即4
,即4 ≥3.∴m≥
≥3.∴m≥ .
.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:
| A、是等比數列 | B、是等差數列 | C、從第2項起是等比數列 | D、是常數列 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3-x |
| 1 | ||
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| 3-x |
| 1 | ||
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| ||
| a-1 |
|
|
|
查看答案和解析>>
科目:高中數學 來源: 題型:
| x |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com