已知極坐標的極點在平面直角坐標系的原點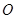
處，極軸與
軸的正半軸重合，且長度單位相同．直線
的極坐標方程為：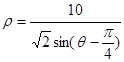
，點
，參數
．
（Ⅰ）求點
軌跡的直角坐標方程；（Ⅱ）求點到直線距離的最大值．
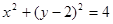（Ⅰ）
；（Ⅱ）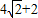
解析試題分析：(Ⅰ)由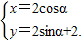
消去θ即求出P軌跡的直角坐標方程；；（Ⅱ）直線l的極坐標方程即為
，化直角坐標方程為x y+10=0，利用直線和圓的位置關系可解．或利用點線距結合三角函數知識求解．
試題解析：（Ⅰ）由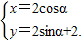且參數α∈[0，2π]，
所以點P的軌跡方程為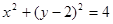．（3分）
（Ⅱ）因為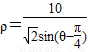
，所以，
所以ρsinθ ρcosθ=10，所以直線l的直角坐標方程為x y+10=0．（6分）
法一：由（Ⅰ） 點P的軌跡方程為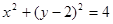，圓心為（0，2），半徑為2.
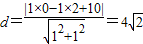，所以點P到直線l距離的最大值 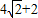.（10分）
法二：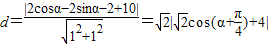
，當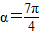
，
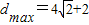，即點P到直線l距離的最大值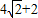．（10分）
考點：1.極坐標方程、普通方程以及轉化；2.點到直線的距離公式
科目：高中數學 來源： 題型：解答題
已知極坐標系的極點與直角坐標系的原點重合，極軸與直角坐標系中
軸的正半軸重合，且兩坐標系有相同的長度單位，圓C的參數方程為
（
為參數），點Q的極坐標為
。
（1）化圓C的參數方程為極坐標方程；
（2）若直線
過點Q且與圓C交于M，N兩點，求當弦MN的長度為最小時，直線的直角坐標方程。
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在平面直角坐標系
中，以
為極點，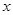
軸非負半軸為極軸建立坐標系，已知曲線
的極坐標方程為
，直線
的參數方程為:
（
為參數），兩曲線相交于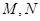
兩點.
（1）寫出曲線的直角坐標方程和直線的普通方程；
（2）若
求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
已知曲線
的極坐標方程是
，以極點為原點，極軸為
軸的正半軸建立平面直角坐標系，直線
的參數方程為
（
為參數）.
（Ⅰ）寫出直線
的普通方程與曲線的直角坐標方程；
（Ⅱ）設曲線經過伸縮變換
得到曲線
，設
為曲線上任一點，求
的最小值，并求相應點
的坐標.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在直角坐標系中，曲線C的參數方程為
（
為參數）.以原點為極點，x軸的正半軸為極軸建立極坐標系，點
，直線l的極坐標方程為
.
（1）判斷點P與直線l的位置關系，說明理由；
（2）設直線l與曲線C的兩個交點為A、B，求
的值.
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
在直角坐標系中，以原點為極點,
軸的正半軸為極軸建立極坐標系,已知曲線
，過點
的直線
的參數方程為：
，(t為參數)，直線與曲線
分別交于
兩點.
(1)寫出曲線和直線的普通方程；
(2)若
成等比數列,求
的值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
以直角坐標系的原點O為極點，x軸的正半軸為極軸，且兩個坐標系取相等的長度單位．已知直線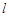
的參數方程為
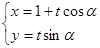(t為參數，0<a<
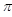)，曲線C的極坐標方程為
．
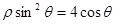（I）求曲線C的直角坐標方程；
（II）設直線l與曲線C相交于A、B兩點，當a變化時，求|AB|的最小值．
查看答案和解析>>
科目：高中數學 來源： 題型：解答題
以原點
為極點，以
軸的正半軸為極軸建立極坐標系，已知曲線
，過點
的直線
的參數方程為
，設直線
與曲線
分別交于
；
（1）寫出曲線和直線
的普通方程；
（2）若
成等比數列,求
的值．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
的直線
，被以原點為極點，
軸的正半軸為極軸，極坐標方程為
的曲線
所截，求截得的弦長．