
【題目】目前,新冠病毒引發的肺炎疫情在全球肆虐,為了解新冠肺炎傳播途徑,采取有效防控措施,某醫院組織專家統計了該地區500名患者新冠病毒潛伏期的相關信息,數據經過匯總整理得到如圖所示的頻率分布直方圖(用頻率作為概率).潛伏期低于平均數的患者,稱為“短潛伏者”,潛伏期不低于平均數的患者,稱為“長潛伏者”.
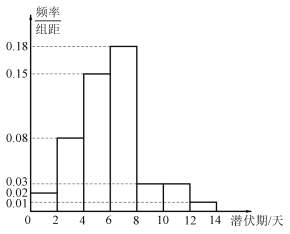
(1)求這500名患者潛伏期的平均數(同一組中的數據用該組區間的中點值作代表),并計算出這500名患者中“長潛伏者”的人數;
(2)為研究潛伏期與患者年齡的關系,以潛伏期是否高于平均數為標準進行分層抽樣,從上述500名患者中抽取300人,得到如下列聯表,請將列聯表補充完整,并根據列聯表判斷是否有97.5%的把握認為潛伏期長短與患者年齡有關;
短潛伏者 | 長潛伏者 | 合計 | |
60歲及以上 | 90 | ||
60歲以下 | 140 | ||
合計 | 300 |
附表及公式:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |

【答案】(1)平均數6;人數250人(2)見解析,有97.5%的把握認為潛伏期長短與年齡有關
【解析】
(1)用各個矩形的面積乘以矩形底邊的中點值再相加即可得到平均數,用樣本容量乘以頻率可得頻數;
(2)根據分層抽樣完善列聯表,根據公式計算出![]() 的值,結合臨界值表可得結論.
的值,結合臨界值表可得結論.
(1)平均數為![]() .
.
“長潛伏者”即潛伏期時間不低于6天的頻率為![]() ,
,
所以500人中“長潛伏者”的人數為![]() 人
人
(2)因為500人中“長潛伏者”的人數為250人,“短潛伏者”的人數為250人,
按分層抽樣可知,300人中“長潛伏者”的人數為150人,“短潛伏者”的人數為150人,
因為60歲及以上的“短潛伏者”的人數為90人,所以60歲以下的“短潛伏者”的人數為60人,
又60歲以下的人數為140人,所以60歲以下的“長潛伏者”的人數為80人,所以60歲及以上的“長潛伏者”的人數為70人,由此可得補充后的列聯表如圖:
短潛伏者 | 長潛伏者 | 合計 | |
60歲及以上 | 90 | 70 | 160 |
60歲以下 | 60 | 80 | 140 |
合計 | 150 | 150 | 300 |
所以![]() 的觀測值為
的觀測值為![]() ,
,
經查表,得![]() ,所以有97.5%的把握認為潛伏期長短與年齡有關.
,所以有97.5%的把握認為潛伏期長短與年齡有關.


 長江作業本同步練習冊系列答案
長江作業本同步練習冊系列答案科目:高中數學 來源: 題型:
【題目】“勾股定理”在西方被稱為“畢達哥拉斯定理”,三國時期吳國的數學家趙爽在《周髀算經》中注釋了其理論證明,其基本思想是圖形經過割補后面積不變.即通過如圖所示的“弦圖”,將勻股定理表述為:“勾股各自乘,并之,為弦實,開方除之,即弦”(其中![]() 分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即
分別為勾股弦);證明方法敘述為:“按弦圖,又可以勾股相乘為朱實二,倍之為朱實四,以勾股之差自相乘為中黃實,加差實,亦成弦實”,即![]() ,化簡得
,化簡得![]() .現已知
.現已知![]() ,
,![]() ,向外圍大正方形
,向外圍大正方形![]() 區域內隨機地投擲一枚飛鏢,飛鏢落在中間小正方形
區域內隨機地投擲一枚飛鏢,飛鏢落在中間小正方形![]() 內的概率是( )
內的概率是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() (
(![]() ,
,![]() )的圖像經過點
)的圖像經過點![]() ,且關于直線
,且關于直線![]() 對稱,則下列結論正確的是( )
對稱,則下列結論正確的是( )
A. ![]() 在
在![]() 上是減函數
上是減函數
B. 函數的最小正周期為![]()
C. ![]() 的解集是
的解集是![]() ,
,![]()
D. ![]() 的一個對稱中心是
的一個對稱中心是![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知拋物線![]() 的頂點在坐標原點,其焦點
的頂點在坐標原點,其焦點![]() 在
在![]() 軸正半軸上,
軸正半軸上,![]() 為直線
為直線![]() 上一點,圓
上一點,圓![]() 與
與![]() 軸相切(
軸相切(![]() 為圓心),且
為圓心),且![]() ,
,![]() 關于點
關于點![]() 對稱.
對稱.
(1)求圓![]() 和拋物線
和拋物線![]() 的標準方程;
的標準方程;
(2)過![]() 的直線
的直線![]() 交圓
交圓![]() 于
于![]() ,
,![]() 兩點,交拋物線
兩點,交拋物線![]() 于
于![]() ,
,![]() 兩點,求證:
兩點,求證:![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】影片《紅海行動》里的“蛟龍突擊隊”在奉命執行撤僑過程中,海軍艦長要求隊員們依次完成6項任務,并對任務的順序提出了如下要求:重點任務A必須排在第2位,且任務E、F必須排在一起,則這6項任務的不同安排方案共有( )
A.18種B.36種C.144種D.216種
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】給定整數![]() (
(![]() ),設集合
),設集合![]() ,記集合
,記集合![]() .
.
(1)若![]() ,求集合
,求集合![]() ;
;
(2)若![]() 構成以
構成以![]() 為首項,
為首項,![]() (
(![]() )為公差的等差數列,求證:集合
)為公差的等差數列,求證:集合![]() 中的元素個數為
中的元素個數為![]() ;
;
(3)若![]() 構成以
構成以![]() 為首項,
為首項,![]() 為公比的等比數列,求集合
為公比的等比數列,求集合![]() 中元素的個數及所有元素之和.
中元素的個數及所有元素之和.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com