
【題目】已知函數![]() .
.
(1)求曲線![]() 在
在![]() 處的切線方程
處的切線方程![]() ,并證明:
,并證明:![]() .
.
(2)當![]() 時,方程
時,方程![]() 有兩個不同的實數根
有兩個不同的實數根![]() ,證明:
,證明:![]() .
.
【答案】(1)![]() ;證明見解析;(2)證明見解析.
;證明見解析;(2)證明見解析.
【解析】
(1)首先求出導函數![]() ,利用導數的幾何意義以及點斜式方程可求切線方程;構造函數
,利用導數的幾何意義以及點斜式方程可求切線方程;構造函數![]() ,利用導數判斷函數的單調性,求出函數的最小值
,利用導數判斷函數的單調性,求出函數的最小值![]() 即證.
即證.
(2)![]() 為方程
為方程![]() 的兩根,不妨設
的兩根,不妨設![]() ,由
,由![]() 在
在![]() 上單調遞增,根據零點存在性定理可知,存在
上單調遞增,根據零點存在性定理可知,存在![]() ,使
,使![]() ,由
,由![]() ,得
,得![]() ,由(1)可得
,由(1)可得![]() ,
,![]() ,然后利用分析法即可證出.
,然后利用分析法即可證出.
解:(1)因為![]() ,
,
所以![]() ,
,![]() , 即切線方程:
, 即切線方程:![]()
下證:![]() ,
,
令![]()
![]() 在
在![]() 上單調遞增,且
上單調遞增,且![]()
所以,![]() 在
在![]() 遞減,在
遞減,在![]() 遞增,
遞增,
所以![]() .
.
所以![]() .
.
(2)![]() ,
,![]() 為方程
為方程![]() 的兩根,
的兩根,
不妨設![]() ,顯然
,顯然![]() 在
在![]() 上單調遞增.
上單調遞增.
且![]() 所以存在
所以存在![]() ,使
,使![]()
當![]() ,
,![]() ,
,![]() 遞減;
遞減;
![]() ,
,![]() ,
,![]() 遞增.
遞增.
由![]() ,得
,得![]() ,又由(1)知
,又由(1)知![]()
所以:![]() ,
,![]()
要證:![]() ,需證:
,需證:![]() ,即證:
,即證:![]()
![]() ,
,![]() ,即證:
,即證:![]() .
.
即:![]()
令![]()
![]()
![]() ,
,
![]() 在
在![]() 單調遞增,且
單調遞增,且![]() .
.
所以,![]() ,
,![]() 在
在![]() 單調遞增.
單調遞增.
所以![]()
所以不等式成立.


科目:高中數學 來源: 題型:
【題目】已知數列![]() 的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有
的首項a1=1,前n項和為Sn.設λ與k是常數,若對一切正整數n,均有![]() 成立,則稱此數列為“λ~k”數列.
成立,則稱此數列為“λ~k”數列.
(1)若等差數列![]() 是“λ~1”數列,求λ的值;
是“λ~1”數列,求λ的值;
(2)若數列![]() 是“
是“![]() ”數列,且an>0,求數列
”數列,且an>0,求數列![]() 的通項公式;
的通項公式;
(3)對于給定的λ,是否存在三個不同的數列![]() 為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
為“λ~3”數列,且an≥0?若存在,求λ的取值范圍;若不存在,說明理由,
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() 是無窮數列.給出兩個性質:
是無窮數列.給出兩個性質:
①對于![]() 中任意兩項
中任意兩項![]() ,在
,在![]() 中都存在一項
中都存在一項![]() ,使
,使![]() ;
;
②對于![]() 中任意項
中任意項![]() ,在
,在![]() 中都存在兩項
中都存在兩項![]() .使得
.使得![]() .
.
(Ⅰ)若![]() ,判斷數列
,判斷數列![]() 是否滿足性質①,說明理由;
是否滿足性質①,說明理由;
(Ⅱ)若![]() ,判斷數列
,判斷數列![]() 是否同時滿足性質①和性質②,說明理由;
是否同時滿足性質①和性質②,說明理由;
(Ⅲ)若![]() 是遞增數列,且同時滿足性質①和性質②,證明:
是遞增數列,且同時滿足性質①和性質②,證明:![]() 為等比數列.
為等比數列.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 、
、![]() 是拋物線
是拋物線![]() 上的兩個不同的點,
上的兩個不同的點,![]() 是坐標原點,若直線
是坐標原點,若直線![]() 與
與![]() 的斜率之積為
的斜率之積為![]() ,則下列結論正確的是( )
,則下列結論正確的是( )
A.![]()
B.以![]() 為直徑的圓面積的最小值為
為直徑的圓面積的最小值為![]()
C.直線![]() 過拋物線
過拋物線![]() 的焦點
的焦點
D.點![]() 到直線
到直線![]() 的距離不大于
的距離不大于![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了響應綠色出行,某市推出了新能源分時租賃汽車,并對該市市民使用新能源租賃汽車的態度進行調查,得到有關數據如下表1:
表1
愿意使用新能源租賃汽車 | 不愿意使用新能源租賃汽車 | 總計 | |
男性 | 100 | 300 | |
女性 | 400 | ||
總計 | 400 |
其中一款新能源分時租賃汽車的每次租車費用由行駛里程和用車時間兩部分構成:行駛里程按1元/公里計費;用車時間不超過30分鐘時,按0.15元/分鐘計費;超過30分鐘時,超出部分按0.20元/分鐘計費.已知張先生從家到上班地點15公里,每天上班租用該款汽車一次,每次的用車時間均在20~60分鐘之間,由于堵車紅綠燈等因素,每次的用車時間![]() (分鐘)是一個隨機變量.張先生記錄了100次的上班用車時間,并統計出在不同時間段內的頻數如下表2:
(分鐘)是一個隨機變量.張先生記錄了100次的上班用車時間,并統計出在不同時間段內的頻數如下表2:
表2
時間 | (20,30] | (30,40] | (40,50] | (50,60] |
頻數 | 20 | 40 | 30 | 10 |
(1)請補填表1中的空缺數據,并判斷是否有99.5%的把握認為該市市民對新能源租賃汽車的使用態度與性別有關;
(2)根據表2中的數據,將各時間段發生的頻率視為概率,以各時間段的區間中點值代表該時間段的取值,試估計張先生租用一次該款汽車上班的平均用車時間;
附: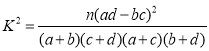
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知![]() ,函數
,函數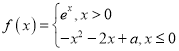 ,則下列說法正確的是( )
,則下列說法正確的是( )
A.若![]() ,則
,則![]() 的圖象上存在唯一一對關于原點
的圖象上存在唯一一對關于原點![]() 對稱的點
對稱的點
B.存在實數![]() 使得
使得![]() 的圖象上存在兩對關于原點
的圖象上存在兩對關于原點![]() 對稱的點
對稱的點
C.不存在實數![]() 使得
使得![]() 的圖象上存在兩對關于
的圖象上存在兩對關于![]() 軸對稱的點
軸對稱的點
D.若![]() 的圖象上存在關于
的圖象上存在關于![]() 軸對稱的點,則
軸對稱的點,則![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】《周髀算經》有這樣一個問題:從冬至日起,依次小寒、大寒、立春、雨水、驚蟄、春分、清明、谷雨、立夏、小滿、芒種十二個節氣日影長減等寸,雨水、驚蟄、春分、清明日影之和為三丈二尺,前七個節氣日影之和為七丈三尺五寸,問立夏日影長為( )
A.七尺五寸B.六尺五寸C.五尺五寸D.四尺五寸
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com