
(2)對于怎樣的整數n,才能由f(sinx)=sinnx推出f(cosx)=cosnx?
(1)證明:f(sinx)=f[cos(![]() -x)]=cos[17(
-x)]=cos[17(![]() -x)]=cos(8π+
-x)]=cos(8π+![]() -17x)=cos(
-17x)=cos(![]() -17x)=sin17x,
-17x)=sin17x,
即f(sinx)=sin17x.
(2)解:f(cosx)=f[sin(![]() -x)]=sin[n(
-x)]=sin[n(![]() -x)]=sin(
-x)]=sin(![]() -nx)
-nx)
=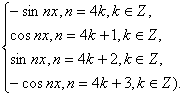
故所求的整數n=4k+1(k∈Z).
點評:正確合理地運用公式是解決問題的關鍵所在.對誘導公式的應用需要較多的思維空間,要善于觀察題目特點,靈活變形.觀察本例條件與結論在結構上類似,差別在于一個含余弦,一個含正弦,注意到正弦、余弦轉化可借助sinx=cos(![]() -x)或cosx=sin(
-x)或cosx=sin(![]() -x).要善于觀察條件和結論的結構特征,找出它們的共性與差異;要注意誘導公式可實現角的形式之間及互余函數名稱之間的轉移.
-x).要善于觀察條件和結論的結構特征,找出它們的共性與差異;要注意誘導公式可實現角的形式之間及互余函數名稱之間的轉移.


科目:高中數學 來源: 題型:
| m |
| n |
| m |
| 3 |
| n |
| π |
| 2 |
| 3 |
查看答案和解析>>
科目:高中數學 來源: 題型:
| 1 |
| 2sin170° |
| π |
| 4 |
| π |
| 2, |
| θ |
| 2 |
| θ |
| 2 |
| 3 |
| θ |
| 2 |
| 3 |
| π |
| 6 |
| π |
| 4 |
| π |
| 3 |
| π |
| 2 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com