Question

【題目】已知四棱錐P-ABCD,底面ABCD是邊長為2的蓌形，PA⊥平面ABCD,PA=2,∠ABC=60°，E,F分別是BC,PC的中點。

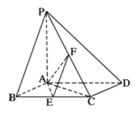
（1）求證：AE⊥PD；

（2）求二面角E-AF-C的余弦值。

Answer 1

【答案】（1）詳見解析（2）

【解析】

試題分析：（Ⅰ）根據(jù)已知條件，容易得出AE⊥BC，AE⊥AD，而PA⊥平面ABCD，所以便可得到AE⊥平面PAD，所以得到AE⊥PD；（Ⅱ）根據(jù)（Ⅰ）可知AE，AD，PA三條直線兩兩垂直，所以可分別以這三條直線分別為x軸，y軸，z軸建立空間直角坐標系，然后分別設(shè)平面AEF，和平面ACF的法向量為

可設(shè)菱形的邊長為2，根據(jù)條件可求出向量的坐標，根據(jù)法向量和這三個向量的垂直關(guān)系即可求出的坐標，所以求這兩個向量夾角的余弦值就可得到二面角E-AF-C的余弦值

試題解析：（Ⅰ）BC=AB，∠ABC=60°，∴AE⊥BC，∴△ABC是等邊三角形；

又E是BC中點，∴AE⊥BC，BC∥AD，∴AE⊥AD；

PA⊥面ABCD，AE平面ABCD，PA⊥AE，即AE⊥PA，AD∩PA=A；

∴AE⊥平面PAD，∴AE⊥PD

（2）以菱形對角線交點為原點建立坐標系更好求點坐標（個人觀點）

＝（,0,0），＝（，，1）

設(shè)平面AEF的一法向量為m=(x1,y1,z1)，則，因此取z1=-1，則m=(0,2,-1)分 因為BD⊥AC，BD⊥PA，PA∩AC=A，所以BD⊥平面AFC，故為平面AFC的一法向量.又=（-,3,0），所以cos＜m,＞=.因為二面角E-AF-C為銳角，所以所求二面角的余弦值為.