
【題目】已知函數(shù)![]() ,
,![]() ,其中
,其中![]() 是自然對數(shù)的底數(shù).
是自然對數(shù)的底數(shù).
(1)求函數(shù)![]() 在[0,π] 上的最大值與最小值;
在[0,π] 上的最大值與最小值;
(2)令![]() ,討論
,討論![]() 的單調性并判斷有無極值,有極值時求出極值.
的單調性并判斷有無極值,有極值時求出極值.
【答案】(1)![]() ;(2)答案見解析.
;(2)答案見解析.
【解析】
(1)求導研究函數(shù)![]() 在[0,π] 上的單調性,進而求出最值;
在[0,π] 上的單調性,進而求出最值;
(2)求出![]() ,并求導可得
,并求導可得![]() ,令
,令![]() ,求導可得函數(shù)
,求導可得函數(shù)![]() 在
在![]() 上單調遞增,進而可得
上單調遞增,進而可得![]() ,對
,對![]() 分類討論:
分類討論:![]() ,
,![]() ,
,![]() ,
,![]() 時,利用導數(shù)研究函數(shù)的單調性和極值即可.
時,利用導數(shù)研究函數(shù)的單調性和極值即可.
解:(1)由已知![]() ,
,
令![]() ,則
,則![]()
此時![]() 恒成立,則
恒成立,則![]() 在
在![]() 上單調遞增,
上單調遞增,
又![]() ,則
,則![]() 在
在![]() 上恒成立,
上恒成立,
![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() ;
;
(2)![]() ,
,
![]()
令![]() ,則
,則![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調遞增,
上單調遞增,
![]() 時,
時,![]() 時,
時,![]() ,
,
①![]() 時,
時,![]() 時,
時,![]() ,
,![]() 時,
時,![]() ,
,
函數(shù)![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,
![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() ;
;
②![]() 時,令
時,令![]() ,
,
解得![]() ,
,
i)![]() 時,
時,
![]() 時,
時,![]() ,
,![]() ,函數(shù)
,函數(shù)![]() 單調遞增;
單調遞增;
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞增;
單調遞增;
![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() ,
,
![]() 時,函數(shù)
時,函數(shù)![]() 取到極大值
取到極大值![]() ;
;
ii) ![]() 時,
時,![]() 時,
時,![]() ,
,
所以函數(shù)![]() 在
在![]() 上單調遞增,無極值;
上單調遞增,無極值;
iii) ![]() 時,
時,![]() ,
,
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞增;
單調遞增;
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞減;
單調遞減;
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 單調遞增,
單調遞增,
![]() 時,函數(shù)
時,函數(shù)![]() 取到極大值
取到極大值![]() ;
;
![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() ;
;
綜上所述:
![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減,
上單調遞減,![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() ;
;
![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() ,
,![]() 時,函數(shù)
時,函數(shù)![]() 取到極大值
取到極大值![]() ;
;
![]() 時,函數(shù)
時,函數(shù)![]() 在
在![]() 上單調遞增,無極值;
上單調遞增,無極值;
![]() 時, 函數(shù)
時, 函數(shù)![]() 在
在![]() ,
,![]() 上單調遞增,在
上單調遞增,在![]() 上單調遞減;
上單調遞減;![]() 時,函數(shù)
時,函數(shù)![]() 取到極大值
取到極大值![]() ;
;![]() 時,函數(shù)
時,函數(shù)![]() 取到極小值
取到極小值![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數(shù)學 來源: 題型:
【題目】已知函數(shù)f(x)=x(lnx-ax)有兩個極值點,則實數(shù)a的取值范圍是( )
A. (-∞,0) B. ![]() C. (0,1) D. (0,+∞)
C. (0,1) D. (0,+∞)
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】已知橢圓![]()
![]() 的離心率為
的離心率為![]() ,兩焦點與短軸的一個端點的連線構成的三角形面積為
,兩焦點與短軸的一個端點的連線構成的三角形面積為![]() .
.
(I)求橢圓![]() 的方程;
的方程;
(II)設與圓![]() 相切的直線
相切的直線![]() 交橢圓
交橢圓![]() 于
于![]() ,
,![]() 兩點(
兩點(![]() 為坐標原點),
為坐標原點),![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某高校在2012年的自主招生考試成績中隨機抽取![]() 名中學生的筆試成績,按成績分組,得到的頻率分布表如表所示.
名中學生的筆試成績,按成績分組,得到的頻率分布表如表所示.
組號 | 分組 | 頻數(shù) | 頻率 |
第1組 |
| 5 |
|
第2組 |
| ① |
|
第3組 |
| 30 | ② |
第4組 |
| 20 |
|
第5組 |
| 10 |
|

(1)請先求出頻率分布表中![]() 位置的相應數(shù)據(jù),再完成頻率分布直方圖;
位置的相應數(shù)據(jù),再完成頻率分布直方圖;
(2)為了能選拔出最優(yōu)秀的學生,高校決定在筆試成績高的第![]() 組中用分層抽樣抽取名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試;
組中用分層抽樣抽取名學生進入第二輪面試,求第3、4、5組每組各抽取多少名學生進入第二輪面試;
(3)在(2)的前提下,學校決定在![]() 名學生中隨機抽取
名學生中隨機抽取![]() 名學生接受
名學生接受![]() 考官進行面試,求:第
考官進行面試,求:第![]() 組至少有一名學生被考官
組至少有一名學生被考官![]() 面試的概率.
面試的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】某研究性學習小組對春季晝夜溫差大小與某花卉種子發(fā)芽多少之間的關系進行研究,他們分別記錄了3月1日至3月5日的每天晝夜溫差與實驗室每天每100顆種子浸泡后的發(fā)芽數(shù),得到如下資料:
日期 | 3月1日 | 3月2日 | 3月3日 | 3月4日 | 3月5日 |
溫差 | 10 | 11 | 13 | 12 | 8 |
發(fā)芽數(shù) | 23 | 25 | 30 | 26 | 16 |
(1)求這5天的平均發(fā)芽率;
(2)從3月1日至3月5日中任選2天,記發(fā)芽的種子數(shù)分別為![]() ,
,![]() ,用
,用![]() 的形式列出所有的基本事件,并求滿足
的形式列出所有的基本事件,并求滿足![]() 的事件
的事件![]() 的概率.
的概率.
查看答案和解析>>
科目:高中數(shù)學 來源: 題型:
【題目】2019年2月13日《煙臺市全民閱讀促進條例》全文發(fā)布,旨在保障全民閱讀權利,培養(yǎng)全民閱讀習慣,提高全民閱讀能力,推動文明城市和文化強市建設.某高校為了解條例發(fā)布以來全校學生的閱讀情況,隨機調查了200名學生每周閱讀時間![]() (單位:小時)并繪制如圖所示的頻率分布直方圖.
(單位:小時)并繪制如圖所示的頻率分布直方圖.
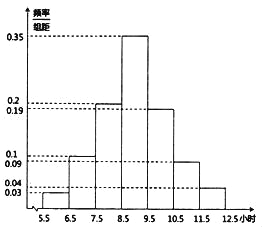
(1)求這200名學生每周閱讀時間的樣本平均數(shù)![]() 和樣本方差
和樣本方差![]() (同一組中的數(shù)據(jù)用該組區(qū)間的中間值代表);
(同一組中的數(shù)據(jù)用該組區(qū)間的中間值代表);
(2)由直方圖可以認為,目前該校學生每周的閱讀時間![]() 服從正態(tài)分布
服從正態(tài)分布![]() ,其中
,其中![]() 近似為樣本平均數(shù)
近似為樣本平均數(shù)![]() ,
,![]() 近似為樣本方差
近似為樣本方差![]() .
.
(i)一般正態(tài)分布的概率都可以轉化為標準正態(tài)分布的概率進行計算:若![]() ,令
,令![]() ,則
,則![]() ,且
,且![]() .利用直方圖得到的正態(tài)分布,求
.利用直方圖得到的正態(tài)分布,求![]() .
.
(ii)從該高校的學生中隨機抽取20名,記![]() 表示這20名學生中每周閱讀時間超過10小時的人數(shù),求
表示這20名學生中每周閱讀時間超過10小時的人數(shù),求![]() (結果精確到0.0001)以及
(結果精確到0.0001)以及![]() 的數(shù)學期望.
的數(shù)學期望.
參考數(shù)據(jù):![]() ,
,![]() .若
.若![]() ,則
,則![]() .
.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com