
【題目】已知圓![]() 過點(diǎn)
過點(diǎn)![]() ,
,![]() ,且圓心
,且圓心![]() 在直線
在直線![]() 上,過點(diǎn)
上,過點(diǎn)![]() 作直線
作直線![]() 與圓
與圓![]() :
:![]() 交于兩點(diǎn)
交于兩點(diǎn)![]() ,
,![]() .
.
(1)求圓![]() 的方程;
的方程;
(2)當(dāng)![]() 時,若
時,若![]() 于圓
于圓![]() 交于
交于![]() ,
,![]() 且
且![]() ,求直線
,求直線![]() 的方程;
的方程;
(3)若點(diǎn)![]() 恰好是線段
恰好是線段![]() 的中點(diǎn),求實數(shù)
的中點(diǎn),求實數(shù)![]() 的取值范圍.
的取值范圍.
【答案】(1)![]() ;(2)
;(2)![]() 或
或![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)設(shè)圓![]() 的方程為:
的方程為:![]() ,代入已知條件求得
,代入已知條件求得![]() 即可;
即可;
(2)驗證直線![]() 斜率不存在時,滿足題意,直線
斜率不存在時,滿足題意,直線![]() 斜率存在時,設(shè)其方程為
斜率存在時,設(shè)其方程為![]() ,由求出兩圓心到直線
,由求出兩圓心到直線![]() 的距離,由勾股定理求得兩弦長,由
的距離,由勾股定理求得兩弦長,由![]() 求得
求得![]() .
.
(3)記![]() 中點(diǎn)為
中點(diǎn)為![]() ,則
,則![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,
,![]() ,由勾股定理得
,由勾股定理得![]() 的關(guān)系,消去
的關(guān)系,消去![]() 后可把
后可把![]() 表示為
表示為![]() 的函數(shù),由
的函數(shù),由![]() 可得
可得![]() 的范圍.
的范圍.
(1)設(shè)圓![]() 的方程為:
的方程為:![]() ,
,
則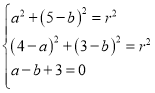 解得
解得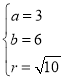 .
.
![]() 圓
圓![]() 的方程為
的方程為![]() .
.
(2)當(dāng)直線![]() 斜率不存在時,直線
斜率不存在時,直線![]() 方程為
方程為![]() ,
,
![]() ,
,![]() ,符合題意;
,符合題意;
直線![]() 斜率存在時,設(shè)直線
斜率存在時,設(shè)直線![]() 的方程為
的方程為![]() ,即
,即![]() ,
,
此時,![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,![]() 到直線
到直線![]() 的距離為
的距離為![]() ,
,
![]() ,
,![]()
![]() .
.
若![]() ,則
,則![]() ,解得
,解得![]() .
.
![]() 直線
直線![]() 的方程為
的方程為![]() .
.
綜上,直線![]() 的方程為
的方程為![]() 或
或![]() .
.
(3)設(shè)![]() 是
是![]() 中點(diǎn),則
中點(diǎn),則![]() ,設(shè)
,設(shè)![]() ,
,![]() ,則
,則![]() ,
,![]() ,
,
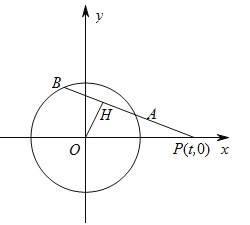
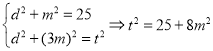 ,
,
又![]() ,
,![]() ,
,
![]() 或
或![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來源: 題型:
【題目】設(shè)函數(shù)![]() 的定義域為
的定義域為![]() ,若存在常數(shù)
,若存在常數(shù)![]() ,使
,使![]() 對一切實數(shù)
對一切實數(shù)![]() 均成立,則稱
均成立,則稱![]() 為“倍約束函數(shù)”
為“倍約束函數(shù)”![]() 現(xiàn)給出下列函數(shù):
現(xiàn)給出下列函數(shù):![]() ;
;![]() ;
;![]() ;
;![]() 是定義在實數(shù)集
是定義在實數(shù)集![]() 上的奇函數(shù),且對一切
上的奇函數(shù),且對一切![]() ,
,![]() 均有
均有![]() 其中是“倍約束函數(shù)”的序號是
其中是“倍約束函數(shù)”的序號是![]()
![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】某網(wǎng)店統(tǒng)計了連續(xù)三天售出商品的種類情況:第一天售出19種商品,第二天售出13種商品,第三天售出18種商品;前兩天都售出的商品有3種,后兩天都售出的商品有4種,則該網(wǎng)店
①第一天售出但第二天未售出的商品有______種;
②這三天售出的商品最少有_______種.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
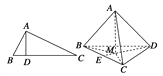
【題目】如圖,在△ABC中,AB⊥AC,若AD⊥BC,則AB2=BD·BC;類似地有命題:在三棱錐A-BCD中,AD⊥平面ABC,若A點(diǎn)在平面BCD內(nèi)的射影為M,則有S![]() =S△BCM·S△BCD.上述命題是 ( )
=S△BCM·S△BCD.上述命題是 ( )
A. 真命題
B. 增加條件“AB⊥AC”才是真命題
C. 增加條件“M為△BCD的垂心”才是真命題
D. 增加條件“三棱錐A-BCD是正三棱錐”才是真命題
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在△ABC中,角A,B,C的對邊分別為a,b,c,若acos2![]() +ccos2
+ccos2![]() =
=![]() b.
b.
(1)求證:a,b,c成等差數(shù)列;
(2)若∠B=60°,b=4,求△ABC的面積.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】學(xué)校藝術(shù)節(jié)對同一類的![]() ,
,![]() ,
,![]() ,
,![]() 四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項參賽作品預(yù)測如下:
四項參賽作品,只評一項一等獎,在評獎揭曉前,甲、乙、丙、丁四位同學(xué)對這四項參賽作品預(yù)測如下:
甲說:“是![]() 或
或![]() 作品獲得一等獎”;
作品獲得一等獎”;
乙說:“![]() 作品獲得一等獎”;
作品獲得一等獎”;
丙說:“![]() ,
,![]() 兩項作品未獲得一等獎”;
兩項作品未獲得一等獎”;
丁說:“是![]() 作品獲得一等獎”.
作品獲得一等獎”.
若這四位同學(xué)中只有兩位說的話是對的,則獲得一等獎的作品是__________.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知![]() ,p:
,p:![]() ,q:
,q:![]() .
.
![]() 已知p是q成立的必要不充分條件,求實數(shù)m的取值范圍;
已知p是q成立的必要不充分條件,求實數(shù)m的取值范圍;
![]() 若
若![]() 是
是![]() 成立的充分不必要條件,求實數(shù)m的取值范圍.
成立的充分不必要條件,求實數(shù)m的取值范圍.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知函數(shù)![]() 滿足如下條件:
滿足如下條件:
①函數(shù)![]() 的最小值為
的最小值為![]() ,最大值為9;
,最大值為9;
②![]() 且
且![]() ;
;
③若函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上是單調(diào)函數(shù),則
上是單調(diào)函數(shù),則![]() 的最大值為2.
的最大值為2.
試探究并解決如下問題:
(Ⅰ)求![]() ,并求
,并求![]() 的值;
的值;
(Ⅱ)求函數(shù)![]() 的圖象的對稱軸方程;
的圖象的對稱軸方程;
(Ⅲ)設(shè)![]() 是函數(shù)
是函數(shù)![]() 的零點(diǎn),求
的零點(diǎn),求![]() 的值的集合.
的值的集合.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com