
 的焦點坐標為
的焦點坐標為 ,過
,過 的直線交拋物線
的直線交拋物線 于
于 兩點,直線
兩點,直線 分別與直線
分別與直線 :
: 相交于
相交于 兩點.
兩點.
 的方程;
的方程;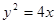 ;(2)證明過程詳見解析.
;(2)證明過程詳見解析.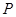 ,代入即可;第二問,討論直線
,代入即可;第二問,討論直線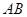 垂直和不垂直
垂直和不垂直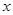 軸2種情況,當直線
軸2種情況,當直線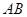 垂直于
垂直于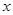 軸時,2個三角形相似,面積比為定值,當直線
軸時,2個三角形相似,面積比為定值,當直線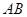 不垂直于
不垂直于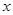 軸時,設出直線
軸時,設出直線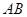 的方程,設出
的方程,設出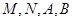 四個點坐標,利用直線
四個點坐標,利用直線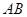 與拋物線相交列出方程組,消參得到方程,利用兩根之積得
與拋物線相交列出方程組,消參得到方程,利用兩根之積得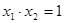 為定值,而面積比值與
為定值,而面積比值與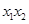 有關,所以也為定值.
有關,所以也為定值.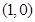 可知
可知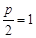
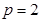 ,所以拋物線
,所以拋物線 的方程為
的方程為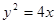 5分
5分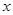 軸時,
軸時,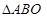 與
與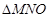 相似,
相似,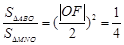 , 7分
, 7分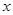 軸不垂直時,設直線AB方程為
軸不垂直時,設直線AB方程為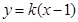 ,
,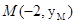 ,
,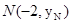 ,
,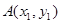 ,
,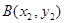 ,
,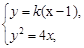 整理得
整理得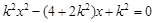 , 9分
, 9分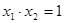 , 10分
, 10分 ,
,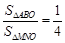 12分
12分

 閱讀快車系列答案
閱讀快車系列答案科目:高中數(shù)學 來源:不詳 題型:單選題
 過拋物線
過拋物線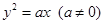 的焦點F,且和
的焦點F,且和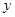 軸交于點A,若△OAF(O為坐標原點)的面積為4,則拋物線方程為( ).
軸交于點A,若△OAF(O為坐標原點)的面積為4,則拋物線方程為( ). 
A.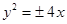 | B.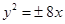 | C.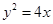 | D.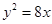 |
查看答案和解析>>
科目:高中數(shù)學 來源:不詳 題型:單選題
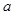 ,則M到y(tǒng)軸距離為 ( )
,則M到y(tǒng)軸距離為 ( )| A.a(chǎn)-p | B.a(chǎn)+p | C.a(chǎn)-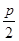 | D.a(chǎn)+2p |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com