
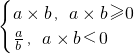 設函數f(x)=lnx⊕x,則f(2)+f(
設函數f(x)=lnx⊕x,則f(2)+f( )=________;若{an}是公比大于0的等比數列,且a5=1,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=a1,則a1=________.
)=________;若{an}是公比大于0的等比數列,且a5=1,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=a1,則a1=________.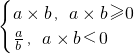 ,∴f(x)=lnx⊕x=
,∴f(x)=lnx⊕x=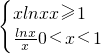 ,
, )=2ln2+
)=2ln2+ =2ln2+2ln
=2ln2+2ln =2ln2-2ln2=0;
=2ln2-2ln2=0; ,
,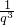 ,
,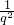 ,
, ,1,q,q2,q3,
,1,q,q2,q3, ,
,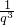 ,
,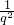 ,
, 均為(0,1)之間的數,
均為(0,1)之間的數,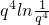 +
+ +
+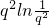 +
+ +0+qlnq+q2lnq2+q3lnq3=-q4lnq4<0,
+0+qlnq+q2lnq2+q3lnq3=-q4lnq4<0, >0矛盾;
>0矛盾; ,
,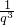 ,
,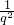 ,
, 均為大于1,
均為大于1, ,
, ,故a1=e
,故a1=e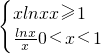 ,代入數值求解可得;可設該數列的前8項分別為
,代入數值求解可得;可設該數列的前8項分別為 ,
,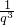 ,
,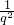 ,
, ,1,q,q2,q3,當q>1時,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=-q4lnq4<0,不合題意,當0<q<1時,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=q4lnq4=
,1,q,q2,q3,當q>1時,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=-q4lnq4<0,不合題意,當0<q<1時,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=q4lnq4= ,解之即可.
,解之即可.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:不詳 題型:填空題
|
| 1 |
| 2 |
查看答案和解析>>
科目:高中數學 來源:2012-2013學年北京市海淀區高三(上)期末數學試卷(文科)(解析版) 題型:填空題
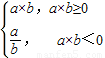 設函數f(x)=lnx⊕x,則f(2)+f(
設函數f(x)=lnx⊕x,則f(2)+f( )= ;若{an}是公比大于0的等比數列,且a5=1,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=a1,則a1= .
)= ;若{an}是公比大于0的等比數列,且a5=1,f(a1)+f(a2)+f(a3)…+f(a7)+f(a8)=a1,則a1= .查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com