
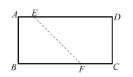
【題目】如圖,在矩形![]() 中,
中,![]() 分別在
分別在![]() 上,且
上,且![]() ,沿
,沿![]() 將四邊形
將四邊形![]() 折成四邊形
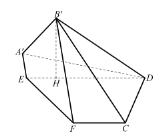
折成四邊形![]() ,使點
,使點![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直線
在直線![]() 上
上
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:![]() 平面
平面![]() ;
;
(3)求二面角![]() 的正弦值
的正弦值
【答案】(1)證明見解析;(2)證明見解析;(3)![]()
【解析】
(1)![]() 平面
平面![]() ,證明故
,證明故![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,得到證明.
,得到證明.
(2)![]() ,
,![]() 得到平面
得到平面![]() 平面
平面![]() ,得到證明.
,得到證明.
(3)以![]() 為
為![]() 軸,平面
軸,平面![]() 內與
內與![]() 垂直的直線為
垂直的直線為![]() 軸,平面
軸,平面![]() 內與
內與![]() 垂直的直線為
垂直的直線為![]() 軸,建立空間直角坐標系,計算
軸,建立空間直角坐標系,計算![]() ,根據
,根據![]() 得到
得到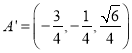 ,平面
,平面![]() 的法向量為
的法向量為![]() ,平面
,平面![]() 的一個法向量為
的一個法向量為![]() ,計算夾角得到答案.
,計算夾角得到答案.
(1)![]() 在平面
在平面![]() 上的射影
上的射影![]() 在直線
在直線![]() 上,故
上,故![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,故
,故![]() ,
,![]() ,
,![]() ,故
,故![]() 平面
平面![]() .
.
![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() .
.
(2)![]() ,故
,故![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() ,
,![]() .
.
故平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,故
,故![]() 平面
平面![]() .
.
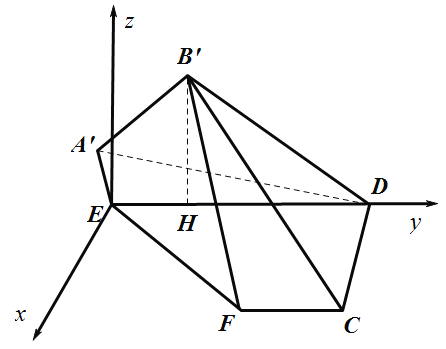
(3)如圖所示:以![]() 為
為![]() 軸,平面
軸,平面![]() 內與
內與![]() 垂直的直線為
垂直的直線為![]() 軸,平面
軸,平面![]() 內與
內與![]() 垂直的直線為
垂直的直線為![]() 軸,建立空間直角坐標系.
軸,建立空間直角坐標系.
![]() ,
,![]() ,
,![]() ,設
,設![]() ,
,![]() ,
,
![]() ,取正解,得到
,取正解,得到![]() ,
,![]() ,故
,故![]() .
.
![]() ,故
,故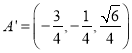 ,
,
設平面![]() 的法向量為
的法向量為![]() ,故
,故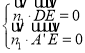 ,即
,即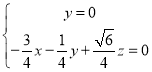 ,
,
取![]() ,得到
,得到![]() ,故
,故![]() .
.
易知:平面![]() 的一個法向量為
的一個法向量為![]() ,故
,故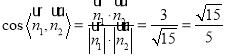 .
.
故二面角![]() 的正弦值為
的正弦值為![]() .
.


 小學生10分鐘口算測試100分系列答案
小學生10分鐘口算測試100分系列答案科目:高中數學 來源: 題型:
【題目】在2019年女排世界杯中,中國女排與巴西女排對壘中采用“五局三勝”制,即哪個隊先勝三場即獲得勝利.根據以往比賽數據統計,中國女排每局獲勝概率為![]() ,巴西女排每局獲勝概率為
,巴西女排每局獲勝概率為![]() .
.
(1)中國女排戰勝巴西女排的概率;
(2)比賽中中國女排第一局獲勝,在該條件下求比賽總局數![]() 的分布列及
的分布列及![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解春季晝夜溫差大小與某種子發芽數之間的關系,現在從4月份的30天中隨機挑選了5天進行研究,且分別記錄了明天晝夜溫差與每天100顆種子浸泡后的發芽數,得到如下表格:
日期 | 4月1日 | 4月7日 | 4月15日 | 4月21日 | 4月30日 |
溫差x/℃ | 10 | 11 | 13 | 12 | 8 |
發芽數y/顆 | 23 | 25 | 30 | 26 | 16 |
從這5天中任選2天,記發芽的種子數分別為![]() ,求事件“
,求事件“![]() 君不小于25”的概率;
君不小于25”的概率;
(2)從這5天中任選2天,若選取的是4月1日與4月30日的兩組數據,請根據這5填中的另三天的數據,求出![]() 關于
關于![]() 的線性回歸方程,
的線性回歸方程,![]() .
.
(參考公式: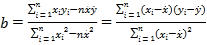 ,
,![]() ).
).
查看答案和解析>>
科目:高中數學 來源: 題型:
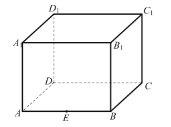
【題目】已知正四棱柱![]() 的底面邊長
的底面邊長![]() ,側棱長
,側棱長![]() ,它的外接球的球心為
,它的外接球的球心為![]() ,點
,點![]() 是
是![]() 的中點,點
的中點,點![]() 是球
是球![]() 上的任意一點,有以下命題:
上的任意一點,有以下命題:
①![]() 的長的最大值為9;
的長的最大值為9;
②三棱錐![]() 的體積的最大值是
的體積的最大值是![]() ;
;
③存在過點![]() 的平面,截球
的平面,截球![]() 的截面面積為
的截面面積為![]() ;
;
④三棱錐![]() 的體積的最大值為20;
的體積的最大值為20;
⑤過點![]() 的平面截球
的平面截球![]() 所得的截面面積最大時,
所得的截面面積最大時,![]() 垂直于該截面.
垂直于該截面.
其中是真命題的序號是___________
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】電動摩托車的續航里程,是指電動摩托車在蓄電池滿電量的情況下一次能行駛的最大距離.為了解A,B兩個不同型號電動摩托車的續航里程,現從某賣場庫存電動摩托車中隨機抽取A,B兩個型號的電動摩托車各5臺,在相同條件下進行測試,統計結果如下:
電動摩托車編號 | 1 | 2 | 3 | 4 | 5 |
A型續航里程(km) | 120 | 125 | 122 | 124 | 124 |
B型續航里程(km) | 118 | 123 | 127 | 120 | a |
已知A,B兩個型號被測試電動摩托車續航里程的平均值相等.
(1)求a的值;
(2)求A型號被測試電動摩托車續航里程標準差的大小;
(3)從被測試的電動摩托車中隨機抽取A,B型號電動摩托車各1臺,求至少有1臺的續航里程超過122km的概率.
(注:n個數據![]() ,的方差
,的方差![]() ,其中
,其中![]() 為數據
為數據![]() 的平均數)
的平均數)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】海水養殖場進行某水產品的新、舊網箱養殖方法的產量對比,收獲時各隨機抽取了![]() 個網箱,測量各水箱產品的產量(單位:kg),其頻率分布直方圖如下圖所示.
個網箱,測量各水箱產品的產量(單位:kg),其頻率分布直方圖如下圖所示.

(1)若用頻率視為概率,記![]() 表示事件“舊養殖法的箱產量低于
表示事件“舊養殖法的箱產量低于![]() kg”,求事件
kg”,求事件![]() 的概率;
的概率;
(2)填寫以下![]() 列聯表,并根據此判斷是否有
列聯表,并根據此判斷是否有![]() 的把握認為箱產量與養殖方法有關?
的把握認為箱產量與養殖方法有關?
箱產量 | 箱產量 | 合計 | |
舊養殖方法 | |||
新養殖方法 | |||
合計 |
(3)根據箱產量頻率分布直方圖,求新養殖法箱產量的中位數的估計值(精確到![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】(本小題滿分12分)已知點![]() 為拋物線
為拋物線![]() 的焦點,點
的焦點,點![]() 在拋物線
在拋物線![]() 上,且
上,且![]() .
.

(Ⅰ)求拋物線![]() 的方程;
的方程;
(Ⅱ)已知點![]() ,延長
,延長![]() 交拋物線
交拋物線![]() 于點
于點![]() ,證明:以點
,證明:以點![]() 為圓心且與直線
為圓心且與直線![]() 相切的圓,必與直線
相切的圓,必與直線![]() 相切.
相切.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知10件不同產品中有3件是次品,現對它們一一取出(不放回)進行檢測,直至取出所有次品為止.
(1)若恰在第5次取到第一件次品,第10次才取到最后一件次品,則這樣的不同測試方法數有多少?
(2)若恰在第6次取到最后一件次品,則這樣的不同測試方法數是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com