
【題目】設AB=6,在線段AB上任取兩點C、D(端點A、B除外),將線段AB分成三條線段AC、CD、DB.
(1)若分成的三條線段的長度均為正整數,求這三條線段可以構成三角形(稱為事件A)的概率;
(2)若分成的三條線段的長度均為正實數,求這三條線段可以構成三角形(稱為事件B)的概率;
(3)根據以下用計算機所產生的20組隨機數,試用隨機數模擬的方法,來近似計算(2)中事件B的概率, 20組隨機數如下:
組別 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
X | 0.52 | 0.36 | 0.58 | 0.73 | 0.41 | 0.6 | 0.05 | 0.32 | 0.38 | 0.73 |
Y | 0.76 | 0.39 | 0.37 | 0.01 | 0.04 | 0.28 | 0.03 | 0.15 | 0.14 | 0.86 |
組別 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 |
X | 0.67 | 0.47 | 0.58 | 0.21 | 0.54 | 0.64 | 0.36 | 0.35 | 0.95 | 0.14 |
Y | 0.41 | 0.54 | 0.51 | 0.37 | 0.31 | 0.23 | 0.56 | 0.89 | 0.17 | 0.03 |
(X和Y都是0~1之間的均勻隨機數)
【答案】
(1)解:若分成的三條線段的長度均為正整數,則三條線段的長度的所有可能為:
1,1,4;1,2,3;1,3,2;1,4,1;
2,1,3;2,2,2;2,3,1;
3,1,2;3,2,1;
4,1,1,
共10種情況,其中只有三條線段為2,2,2時能構成三角形
則構成三角形的概率p= ![]()
(2)解:由題意知本題是一個幾何概型
設其中兩條線段長度分別為x,y,
則第三條線段長度為6﹣x﹣y,
則全部結果所構成的區域為:
0<x<6,0<y<6,0<6﹣x﹣y<6,
即為0<x<6,0<y<6,0<x+y<6
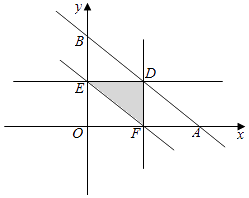
所表示的平面區域為三角形OAB;
若三條線段x,y,6﹣x﹣y,能構成三角形,
則還要滿足 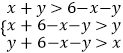 ,即為
,即為 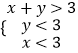 ,
,
所表示的平面區域為三角形DEF,
由幾何概型知所求的概率為:P= ![]() =
= ![]()
(3)解:步驟如下:
①產生兩組0~1之間的均勻隨機數X、Y(題目給出)
②經平移和伸縮變換,a=6X,b=6Y,
③數出落在0<x<6,0<y<6,0<6﹣x﹣y<6的點(a,b)的個數N和落在0<x<3,0<y<3,0<6﹣x﹣y<6,6﹣x﹣y+y>x,x+y>6﹣x﹣y
的點(a,b)的個數N1,由已知中的20組隨機數可數得N=13,N1=3
④由 ![]() =
= ![]() ,故P(B)=
,故P(B)= ![]() .
.
【解析】(1)本題是一個古典概型,若分成的三條線段的長度均為正整數,則三條線段的長度的所有可能為:1,1,4;1,2,3;2,2,2共3種情況,其中只有三條線段為2,2,2時能構成三角形,得到概率.(2)本題是一個幾何概型,設出變量,寫出全部結果所構成的區域,和滿足條件的事件對應的區域,注意整理三條線段能組成三角形的條件,做出面積,做比值得到概率.(3)根據隨機數模擬的方法和步驟即可近似計算(2)中事件B的概率.
【考點精析】關于本題考查的幾何概型,需要了解幾何概型的特點:1)試驗中所有可能出現的結果(基本事件)有無限多個;2)每個基本事件出現的可能性相等才能得出正確答案.


科目:高中數學 來源: 題型:
【題目】某地區2007年至2013年農村居民家庭純收入y(單位:千元)的數據如下表:
年份 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 |
年份代號t | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人均純收入y | 2.9 | 3.3 | 3.6 | 4.4 | 4.8 | 5.2 | 5.9 |
(1)求y關于t的線性回歸方程;
(2)利用(1)中的回歸方程,分析2007年至2013年該地區農村居民家庭人均純收入的變化情況,并預測該地區2015年農村居民家庭人均純收入.
附:回歸直線的斜率和截距的最小二乘法估計公式分別為:
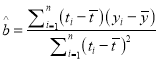 ,
, ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某品牌手機廠商推出新款的旗艦機型,并在某地區跟蹤調查得到這款手機上市時間(第x周)和市場占有率(y﹪)的幾組相關數據如下表:
| 1 | 2 | 3 | 4 | 5 |
| 0.03 | 0.06 | 0.1 | 0.14 | 0.17 |
(Ⅰ)根據表中的數據,用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程
的線性回歸方程![]() ;
;
(Ⅱ)根據上述線性回歸方程,分析該款旗艦機型市場占有率的變化趨勢,并預測在第幾周,該款旗艦機型市場占有率將首次超過 0.40﹪(最后結果精確到整數).
參考公式: ,
,![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將參加數學競賽的1000名學生編號如下:0001,0002,0003,…,1000,打算從中抽取一個容量為50的樣本,按系統抽樣的辦法分成50個部分.如果第一部分編號為0001,0002,…,0020,從中隨機抽取一個號碼為0015,則第40個號碼為
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某大學藝術專業400名學生參加某次測評,根據男女學生人數比例,使用分層抽樣的方法從中隨機抽取了100名學生,記錄他們的分數,將數據分成7組:[20,30),[30,40),┄,[80,90],并整理得到如下頻率分布直方圖:
(Ⅰ)從總體的400名學生中隨機抽取一人,估計其分數小于70的概率;
(Ⅱ)已知樣本中分數小于40的學生有5人,試估計總體中分數在區間[40,50)內的人數;
(Ⅲ)已知樣本中有一半男生的分數不小于70,且樣本中分數不小于70的男女生人數相等.試估計總體中男生和女生人數的比例.

查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知圓O:x2+y2=4,直線l:12x-5y+c=0(其中c為常數).下列有關直線l與圓O的命題中正確命題的序號是________.
①當c=0時,圓O上有四個不同的點到直線l的距離為1;
②若圓O上有四個不同的點到直線l的距離為1,則-13<c<13;
③若圓O上恰有三個不同的點到直線l的距離為1,則c=13;
④若圓O上恰有兩個不同的點到直線l的距離為1,則13<c<39;
⑤當c=±39時,圓O上只有一個點到直線l的距離為1.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com