|
|
|
已知數列{an}中，a1＝1，a2＝3，an+2＝3an+1－2an(n∈N*)．
(1)設bn＝an+1－2an，求證：數列{bn}是常數列，并寫出其通項公式；
(2)設cn＝an+1－an，求證：數列{cn}是等比數列，并寫出其通項公式；
(3)求數列{an}的通項公式．
|
|
|
練習冊系列答案
相關習題
科目：高中數學
來源：人民教育出版社 代數
題型：
|
|
|
若扇形的圓心角是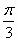 ，半徑為R，則扇形的內切圓面積與扇形的面積之為
|
| [ ] |
A． |
1∶2
|
B． |
1∶3
|
C． |
2∶3
|
D． |
3∶4
|
|
|
查看答案和解析>>
科目：高中數學
來源：人民教育出版社 平面解析幾何
題型：
|
|
|
已知△ABC中，A(4，2)，B(1，8)，C(－1，8)．
(1)求AB邊上的高所在的直線方程；
(2)直線l∥AB，與AC，BC依次交于E，F，S△CEF∶S△ABC＝1∶4．求l所在的直線方程．
|
|
|
查看答案和解析>>
科目：高中數學
來源：人民教育出版社（實驗修訂本） 高中數學
題型：
|
|
|
已知數列{an}，{bn}都是等比數列，那么
|
| [ ] |
A． |
數列{an＋bn}，{an·bn}都一定是等比數列
|
B． |
數列{an＋bn}一定是等比數列，數列{an·bn}不一定是等比數列
|
C． |
數列{an＋bn}不一定是等比數列，數列{an·bn}一定是等比數列
|
D． |
數列{an＋bn}，{an·bn}都不一定是等比數列
|
|
|
查看答案和解析>>
科目：高中數學
來源：人民教育出版社（實驗修訂本） 高中數學
題型：
|
|
|
在等比數列{an}中，a1＋a2＝3，a2＋a3＝6，則a3＋a4＝
|
| [ ] |
A． |
－12
|
B． |
12
|
C． |
9
|
D． |
－9
|
|
|
查看答案和解析>>
科目：高中數學
來源：人民教育出版社（實驗修訂本） 高中數學
題型：
|
|
|
已知等差數列{an}中，a2＝2，a1＋a4＝5，
(1)求數列{an}的通項公式；
(2)若bn＝2nan，求數列{bn}的前n項和Sn．
|
|
|
查看答案和解析>>
科目：高中數學
來源：人教B版（新課標） 必修2
題型：
|
|
|
如圖，在三棱錐P－ABC中，AB⊥BC，AB＝BC＝kPA，點O、D分別是AC、PC的中點，OP⊥底面ABC．
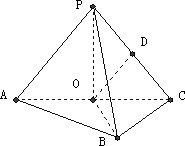
(1)當k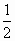＝ 時，求直線PA與BC所成角的余弦值；
(2)當k＝ 時，求二面角A－PC－B的正弦值；
(3)當k取何值時，O在平面PBC內的射影恰好為△PBC的重心？
|
|
|
查看答案和解析>>
、
是平面內兩個互相垂直的單位向量，若向量
滿足(
＝(a，cosB)，
＝(b，cosA)，且