
【題目】實數m取什么值時,復平面內表示復數z=(m2-8m+15)+(m2-5m-14)i的點.
(1)位于第四象限?
(2)位于第一、三象限?
(3)位于直線y=x上?
【答案】(1)![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() 或
或![]() ;(3)
;(3)![]()
【解析】
試題(1)由題意得,復數位于第四象限,則實部大于![]() ,虛部小于
,虛部小于![]() ,列出方程組即可求解實數
,列出方程組即可求解實數![]() 的取值范圍;
的取值范圍;
(2)根據復數的定義和復數的表示,列出不等式組,即可求解實數![]() 的取值范圍;
的取值范圍;
(3)使得復數位于直線![]() 上,只需實部與虛部相等即可求解實數
上,只需實部與虛部相等即可求解實數![]() 的值.
的值.
試題解析:
(1)由![]()
![]()
解得-2<m<3或5<m<7,此時復數z對應的點位于第四象限.
(2)由![]() 或
或![]()
可等價轉化為(m2-8m+15)(m2-5m-14)>0,即(m-3)(m-5)(m+2)(m-7)>0,
利用“數軸標根法”可得:m<-2或3<m<5或m>7,此時復數z對應的點位于第一、三象限.
(3)要使點Z在直線y=x上,需m2-8m+15=m2-5m-14,解得m=![]() .此時,復數z對應的點位于直線y=x上.
.此時,復數z對應的點位于直線y=x上.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:高中數學 來源: 題型:
【題目】如圖所示,某鐵制零件由一個正四棱柱和一個球組成,已知正四棱柱底面邊長與球的直徑均為1cm,正四棱柱的高為2cm.現有這種零件一盒共50kg,取鐵的密度為![]() ,
,![]() .
.
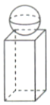
(1)估計有多少個這樣的零件;
(2)如果要給這盒零件的每個零件表面涂上一種特殊的材料,則需要能涂多少平方厘米的材料(球與棱柱接口處的面積不計,結果精確到![]() )?
)?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某工廠生產甲,乙兩種圖畫紙,計劃每種圖畫紙的生產量不少于8t,已知生產甲種圖畫紙1t要用蘆葦7t、黃麻3t、楓樹5t;生產乙種圖畫紙1t要用蘆葦3t、黃麻4t、楓樹8 t.現在倉庫內有蘆葦300t、黃麻150t.楓樹200t,試列出滿足題意的不等式組.
查看答案和解析>>
科目:高中數學 來源: 題型:
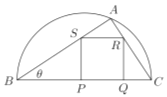
【題目】校園準備綠化一塊直徑為![]() 的半圓形空地,點
的半圓形空地,點![]() 在半圓圓弧上,△
在半圓圓弧上,△![]() 外的地方種草,△
外的地方種草,△![]() 的內接正方形
的內接正方形![]() 為一水池(
為一水池(![]() ,
,![]() 在
在![]() 邊上),其余地方種花,若
邊上),其余地方種花,若![]() ,
, ![]() ,設△
,設△![]() 的面積為
的面積為![]() ,正方形面積為
,正方形面積為![]() ;
;
(1)用![]() 和
和![]() 表示
表示![]() 和
和![]() ;
;
(2)當![]() 固定,
固定,![]() 變化時,求
變化時,求![]() 最小值及此時的角
最小值及此時的角![]() ;
;
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某商場按月訂購一種家用電暖氣,每銷售一臺獲利潤200元,未銷售的產品返回廠家,每臺虧損50元,根據往年的經驗,每天的需求量與當天的最低氣溫有關,如果最低氣溫位于區間![]() ,需求量為100臺;最低氣溫位于區間
,需求量為100臺;最低氣溫位于區間![]() ,需求量為200臺;最低氣溫位于區間
,需求量為200臺;最低氣溫位于區間![]() ,需求量為300臺。公司銷售部為了確定11月份的訂購計劃,統計了前三年11月份各天的最低氣溫數據,得到下面的頻數分布表:
,需求量為300臺。公司銷售部為了確定11月份的訂購計劃,統計了前三年11月份各天的最低氣溫數據,得到下面的頻數分布表:
最低氣溫(℃) |
|
|
|
|
|
天數 | 11 | 25 | 36 | 16 | 2 |
以最低氣溫位于各區間的頻率代替最低氣溫位于該區間的概率.
求11月份這種電暖氣每日需求量![]() (單位:臺)的分布列;
(單位:臺)的分布列;
若公司銷售部以每日銷售利潤![]() (單位:元)的數學期望為決策依據,計劃11月份每日訂購200臺或250臺,兩者之中選其一,應選哪個?
(單位:元)的數學期望為決策依據,計劃11月份每日訂購200臺或250臺,兩者之中選其一,應選哪個?
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數),
為參數),![]() ,
,![]() 為曲線
為曲線![]() 上的一動點.
上的一動點.
(I)求動點![]() 對應的參數從
對應的參數從![]() 變動到
變動到![]() 時,線段
時,線段![]() 所掃過的圖形面積;
所掃過的圖形面積;
(Ⅱ)若直線![]() 與曲線
與曲線![]() 的另一個交點為
的另一個交點為![]() ,是否存在點
,是否存在點![]() ,使得
,使得![]() 為線段
為線段![]() 的中點?若存在,求出點
的中點?若存在,求出點![]() 坐標;若不存在,說明理由.
坐標;若不存在,說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com