
【題目】已知等差數列{an}中,a2=5,S5=40.等比數列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通項公式
(2)令cn=anbn,求數列{cn}的前n項和Tn.
【答案】(1)an=3n﹣1;(2)![]() ;(3)
;(3)![]()
【解析】試題分析:(1)設出數列的公差,分別根據等差數列的通項公式表示出![]() 和
和![]() 聯立方程求得和
聯立方程求得和![]() 和
和![]() ,則數列的通項公式可得,求出首項與公比,即可得
,則數列的通項公式可得,求出首項與公比,即可得![]() 的通項公式;(2)由(1)得的
的通項公式;(2)由(1)得的![]() 代入
代入![]() ,利用錯位相減求和即可.
,利用錯位相減求和即可.
試題解析:(1)設公差為d,則由a2=5,S5=40,得:![]() ,解得
,解得![]() ,則an=3n﹣1…
,則an=3n﹣1…
∵![]() ∴q=3
∴q=3![]() …
…
(2)![]() ①
①
∴![]() ②
②
①﹣②:![]()
∴![]() …
…
【 方法點睛】本題主要考查等比數列和等差數列的通項以及錯位相減法求數列的的前![]() 項和,屬于中檔題.一般地,如果數列
項和,屬于中檔題.一般地,如果數列![]() 是等差數列,
是等差數列,![]() 是等比數列,求數列
是等比數列,求數列![]() 的前
的前![]() 項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列
項和時,可采用“錯位相減法”求和,一般是和式兩邊同乘以等比數列![]() 的公比,然后作差求解, 在寫出“
的公比,然后作差求解, 在寫出“![]() ”
”![]() 與“
與“![]() ” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“
” 的表達式時應特別注意將兩式“錯項對齊”以便下一步準確寫出“![]() ”的表達式.
”的表達式.


科目:高中數學 來源: 題型:
【題目】已知二次函數![]() 的對稱軸為
的對稱軸為![]() ,
,![]() .
.
(1)求函數![]() 的最小值及取得最小值時
的最小值及取得最小值時![]() 的值;
的值;
(2)試確定![]() 的取值范圍,使
的取值范圍,使![]() 至少有一個實根;
至少有一個實根;
(3)當![]() 時,
時,![]() ,對任意
,對任意![]() 有
有![]() 恒成立,求實數
恒成立,求實數![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 是菱形,
是菱形,![]() ,側面
,側面![]() 是邊長為2的等邊三角形,點
是邊長為2的等邊三角形,點![]() 是
是![]() 的中點,且平面
的中點,且平面![]() 平面
平面![]() .
.
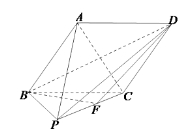
(I)求異面直線![]() 與
與![]() 所成角的余弦值;
所成角的余弦值;
(II)若點![]() 在線段
在線段![]() 上移動,是否存在點
上移動,是否存在點![]() 使平面
使平面![]() 與平面
與平面![]() 所成的角為
所成的角為![]() ?若存在,指出點
?若存在,指出點![]() 的位置,否則說明理由.
的位置,否則說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】據俄羅斯新羅西斯克2015年5月17日電 記者吳敏、鄭文達報道:當地時間17日,參加中俄“海上聯合-2015(Ⅰ)”軍事演習的9艘艦艇抵達地中海預定海域,混編組成海上聯合集群.接到命令后我軍在港口M要將一件重要物品用小艇送到一艘正在航行的俄軍輪船上,在小艇出發時,輪船位于港口M北偏西30°且與該港口相距20海里的A處,并正以30海里/小時的航行速度沿正東方向勻速行駛.假設該小艇沿直線方向以v海里/小時的航行速度勻速行駛,經過t小時與輪船相遇.
(1)若希望相遇時小艇的航行距離最小,則小艇航行速度的大小應為多少?
(2)為保證小艇在30分鐘內(含30分鐘)能與輪船相遇,試確定小艇航行速度的最小值并說明你的推理過程;
(3)是否存在v,使得小艇以v海里/小時的航行速度行駛,總能有兩種不同的航行方向與輪船相遇?若存在,試確定v的取值范圍;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知隨機變量X~N(μ,σ2),且其正態曲線在(-∞,80)上是增函數,在(80,+∞)上為減函數,且P(72≤X≤88)=0.682 6.
(1)求參數μ,σ的值;
(2)求P(64<X≤72).
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設![]() 實數
實數![]() 滿足不等式
滿足不等式![]() 函數
函數![]() 無極值點.
無極值點.
(1)若“![]() ”為假命題,“
”為假命題,“![]() ”為真命題,求實數
”為真命題,求實數![]() 的取值范圍;
的取值范圍;
(2)已知“![]() ”為真命題,并記為
”為真命題,并記為![]() ,且
,且![]() ,若
,若![]() 是
是![]() 的必要不充分條件,求正整數
的必要不充分條件,求正整數![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
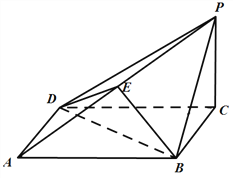
【題目】如圖,在四棱錐![]() 中,底面
中,底面![]() 為正方形,點
為正方形,點![]() 是棱
是棱![]() 的中點,
的中點,![]() ,平面
,平面![]()
![]() 平面
平面![]() .
.
(Ⅰ)求證:![]() //平面
//平面![]() ;
;
(Ⅱ)求證:![]() 平面
平面![]() ;
;
(Ⅲ) 設![]() ,試判斷平面
,試判斷平面![]() ⊥平面
⊥平面![]() 能否成立;若成立,寫出
能否成立;若成立,寫出![]() 的一個值(只需寫出結論).
的一個值(只需寫出結論).
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com