
【題目】已知函數(shù)![]() ,
,![]() ,曲線
,曲線![]() 與
與![]() 在原點處有公共切線.
在原點處有公共切線.
(I)若![]() 為函數(shù)的極大值點,求
為函數(shù)的極大值點,求![]() 的單調(diào)區(qū)間(用
的單調(diào)區(qū)間(用![]() 表示);
表示);
(II)若![]() ,
,![]() ,求
,求![]() 的取值范圍.
的取值范圍.
【答案】(Ⅰ)單調(diào)遞增區(qū)間為![]() ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為![]() ,
,![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
試題分析:(Ⅰ)首先分別求出![]() ,然后利用導(dǎo)數(shù)的幾何意義求得
,然后利用導(dǎo)數(shù)的幾何意義求得![]() ,由此對分
,由此對分![]() 、
、![]() 利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性即可得出;(Ⅱ)首先利用導(dǎo)數(shù)得到函數(shù)
利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性即可得出;(Ⅱ)首先利用導(dǎo)數(shù)得到函數(shù)![]() 的單調(diào)性,由此得到
的單調(diào)性,由此得到![]() 的最小值,從而得到
的最小值,從而得到![]() ,設(shè)
,設(shè)![]() ,然后分
,然后分![]() 、
、![]() 、
、![]() ,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性即可得出.
,利用導(dǎo)數(shù)研究函數(shù)的單調(diào)性即可得出.
試題解析:(I)由題意知:![]() 的定義域為
的定義域為![]() ,且
,且![]() ,
,![]() ,
,
因為曲線![]() 與
與![]() 在原點處有公共的切線,故
在原點處有公共的切線,故![]() ,
,
解得:![]() ,………………2分
,………………2分
所以![]() ,
,
![]() .………………3分
.………………3分
![]() 時,
時,![]() ,函數(shù)
,函數(shù)![]() 在定義域上是減函數(shù),故不滿足題意;4分
在定義域上是減函數(shù),故不滿足題意;4分
![]() 時,因為
時,因為![]() 為函數(shù)
為函數(shù)![]() 的極大值點,故由
的極大值點,故由![]() 的圖象可知
的圖象可知![]() ,
,
由![]() 得:
得:![]() ,由
,由![]() 得:
得:![]() .
.
所以函數(shù)![]() 的單調(diào)遞增區(qū)間為
的單調(diào)遞增區(qū)間為![]() ,單調(diào)遞減區(qū)間為
,單調(diào)遞減區(qū)間為![]() ,
,![]() .………………6分
.………………6分
(II)因為![]() ,且
,且![]() 時
時![]() ,
,![]() 時
時![]() ,
,
故![]() 時,
時,![]() 取得最小值0,所以
取得最小值0,所以![]() ,即
,即![]() ,從而
,從而![]() .
.
設(shè)![]() ,
,
則![]() .………………7分
.………………7分
①當(dāng)![]() 時,因為
時,因為![]() ,所以
,所以![]() ,
,
所以![]() 在
在![]() 上單調(diào)遞增,從而
上單調(diào)遞增,從而![]() ,即
,即![]() ,所以
,所以![]() .………………9分
.………………9分
②當(dāng)![]() 時,由①知
時,由①知![]() ,
,
所以![]() ,故
,故![]() ,即
,即![]() .……11分
.……11分
③當(dāng)![]() 時,令
時,令![]() ,則
,則![]() ,
,
顯然![]() 在
在![]() 上單調(diào)遞增,又
上單調(diào)遞增,又![]() ,
,![]() ,
,
所以![]() 在
在![]() 上存在唯一零點
上存在唯一零點![]() ,
,
當(dāng)![]() 時,
時,![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
從而![]() ,即
,即![]() ,所以
,所以![]() 在
在![]() 上單調(diào)遞減,
上單調(diào)遞減,
從而當(dāng)![]() 時,
時,![]() ,即
,即![]() ,不合題意.………………13分
,不合題意.………………13分
綜上,實數(shù)![]() 的取值范圍為
的取值范圍為![]() .………………14分
.………………14分


 全能測控期末小狀元系列答案
全能測控期末小狀元系列答案科目:高中數(shù)學(xué) 來源: 題型:
【題目】成等差數(shù)列的三個正數(shù)的和等于15,并且這三個數(shù)分別加上2、5、13后成為等比數(shù)列{bn}中的b3、b4、b5.
(Ⅰ)求數(shù)列{bn}的通項公式;
(Ⅱ)數(shù)列{bn}的前n項和為Sn,求證:數(shù)列{Sn+![]() }是等比數(shù)列.
}是等比數(shù)列.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】為方便市民休閑觀光,市政府計劃在半徑為200米,圓心角為![]() 的扇形廣場內(nèi)(如圖所示),沿
的扇形廣場內(nèi)(如圖所示),沿![]() 邊界修建觀光道路,其中
邊界修建觀光道路,其中![]() 分別在線段
分別在線段![]() 上,且
上,且![]() 兩點間距離為定長
兩點間距離為定長![]() 米.
米.
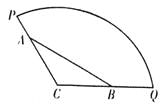
(1)當(dāng)![]() 時,求觀光道
時,求觀光道![]() 段的長度;
段的長度;
(2)為提高觀光效果,應(yīng)盡量增加觀光道路總長度,試確定圖中![]() 兩點的位置,使觀光道路總長度達到最長?并求出總長度的最大值.
兩點的位置,使觀光道路總長度達到最長?并求出總長度的最大值.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】在一次籃球定點投籃訓(xùn)練中,規(guī)定每人最多投3次,在![]() 處每投進一球得3分;在
處每投進一球得3分;在![]() 處每投進一球得2分,如果前兩次得分之和超過3分就停止投籃;否則投第3次,某同學(xué)在
處每投進一球得2分,如果前兩次得分之和超過3分就停止投籃;否則投第3次,某同學(xué)在![]() 處的抽中率
處的抽中率![]() ,在
,在![]() 處的抽中率為
處的抽中率為![]() ,該同學(xué)選擇現(xiàn)在
,該同學(xué)選擇現(xiàn)在![]() 處投第一球,以后都在
處投第一球,以后都在![]() 處投,且每次投籃都互不影響,用
處投,且每次投籃都互不影響,用![]() 表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分,其分布列為:
表示該同學(xué)投籃訓(xùn)練結(jié)束后所得的總分,其分布列為:
| 0 | 2 | 3 | 4 | 5 |
| 0.03 |
|
|
|
|
(1)求![]() 的值;
的值;
(2)求隨機變量![]() 的數(shù)學(xué)期望
的數(shù)學(xué)期望![]() ;
;
(3)試比較該同學(xué)選擇上述方式投籃得分超過3分與選擇都在![]() 處投籃得分超過3分的概率的大小.
處投籃得分超過3分的概率的大小.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】根據(jù)微信同程旅游的調(diào)查統(tǒng)計顯示,參與網(wǎng)上購票的1000位購票者的年齡(單位:歲)情況如圖所示.
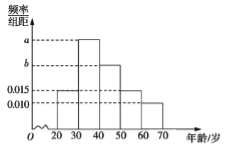
(1)已知中間三個年齡段的網(wǎng)上購票人數(shù)成等差數(shù)列,求![]() 的值;
的值;
(2)為鼓勵大家網(wǎng)上購票,該平臺常采用購票就發(fā)放酒店入住代金券的方法進行促銷,具體做法如下:
年齡在![]() 歲的每人發(fā)放20元,其余年齡段的每人發(fā)放50元,先按發(fā)放代金券的金額采用分層抽樣的方式從參與調(diào)查的1000位網(wǎng)上購票者中抽取5人,并在這5人中隨機抽取3人進行回訪調(diào)查,求此3人獲得代金券的金額總和為90元的概率.
歲的每人發(fā)放20元,其余年齡段的每人發(fā)放50元,先按發(fā)放代金券的金額采用分層抽樣的方式從參與調(diào)查的1000位網(wǎng)上購票者中抽取5人,并在這5人中隨機抽取3人進行回訪調(diào)查,求此3人獲得代金券的金額總和為90元的概率.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】已知等差數(shù)列{an}中,a2=5,S5=40.等比數(shù)列{bn}中,b1=3,b4=81,
(1)求{an}和{bn}的通項公式
(2)令cn=anbn,求數(shù)列{cn}的前n項和Tn.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】從甲、乙兩名學(xué)生中選拔一人參加射箭比賽,為此需要對他們的射箭水平進行測試.現(xiàn)這兩名學(xué)生在相同條件下各射箭10次,命中的環(huán)數(shù)如下:
甲 | 8 | 9 | 7 | 9 | 7 | 6 | 10 | 10 | 8 | 6 |
乙 | 10 | 9 | 8 | 6 | 8 | 7 | 9 | 7 | 8 | 8 |
(1)計算甲、乙兩人射箭命中環(huán)數(shù)的平均數(shù)和標準差;
(2)比較兩個人的成績,然后決定選擇哪名學(xué)生參加射箭比賽.
查看答案和解析>>
科目:高中數(shù)學(xué) 來源: 題型:
【題目】如圖,在四棱錐![]() 中,
中,![]() 平面
平面![]() ,四邊形
,四邊形![]() 為正方形,點
為正方形,點![]() 分別為線段
分別為線段![]() 上的點,
上的點,![]() .
.
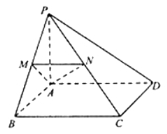
(1)求證:平面![]() 平面
平面![]() ;
;
(2)求證:當(dāng)點![]() 不與點
不與點![]() 重合時,
重合時,![]() 平面
平面![]() ;
;
(3)當(dāng)![]() ,
,![]() 時,求點
時,求點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com