
【題目】已知二次函數![]() 的最小值為1,且
的最小值為1,且![]() .
.
(1)求![]() 的解析式;
的解析式;
(2)若![]() 在區間
在區間![]() 上不單調,求實數m的取值范圍;
上不單調,求實數m的取值范圍;
(3)求函數![]() 在區間
在區間![]() 上的最小值
上的最小值![]() .
.
【答案】(1) ![]() ,(2)
,(2) ![]() ,(3)
,(3) 
【解析】
(1)根據題意設出![]() ,將f(0)=3代入,可得f(x)的解析式;
,將f(0)=3代入,可得f(x)的解析式;
(2)若f(x)在區間[3m,m+2]上不單調,則1∈(3m,m+2),解得實數m的取值范圍;
(3)結合二次函數的圖象和性質,分析各種情況下函數f(x)在區間[t﹣1,t]上的最小值g(t),綜合討論結果,可得答案.
(1)![]() ,
,
∴函數圖象關于直線![]() 對稱,
對稱,
又∵二次函數![]() 的最小值為1,
的最小值為1,
∴設![]() ,
,
由![]() 得:
得:![]() ,
,
故![]()
(2)要使函數在區間![]() 上不單調,
上不單調,
則![]() ,
,
解得:![]()
(3)由(1)知![]() ,
,
所以函數![]() 圖象開口向上,對稱軸方程為
圖象開口向上,對稱軸方程為![]() ,
,
①當![]() 即
即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞增,
上單調遞增,
當![]() 時
時![]() 的最小值
的最小值![]() ,
,
②當![]() .即
.即![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞減,在區間
上單調遞減,在區間![]() 上單調遞增,
上單調遞增,
當![]() 時,
時,![]() 的最小值
的最小值![]() ,
,
③當![]() 時,函數
時,函數![]() 在區間
在區間![]() 上單調遞減,
上單調遞減,
當![]() 時,
時,![]() 的最小值
的最小值![]() ,
,
綜上所述,


 亮點激活精編提優100分大試卷系列答案
亮點激活精編提優100分大試卷系列答案科目:高中數學 來源: 題型:
【題目】山西省在2019年3月份的高三適應性考試中對數學成績數據統計顯示,全市10000名學生的成績近似服從正態分布![]() ,現某校隨機抽取了50名學生的數學成績分析,結果這50名學生的成績全部介于85分到145分之間,現將結果按如下方式分為6組,第一組
,現某校隨機抽取了50名學生的數學成績分析,結果這50名學生的成績全部介于85分到145分之間,現將結果按如下方式分為6組,第一組![]() ,第二組
,第二組![]() ,…,第六組
,…,第六組![]() ,得到如圖所示的頻率分布直方圖:
,得到如圖所示的頻率分布直方圖:
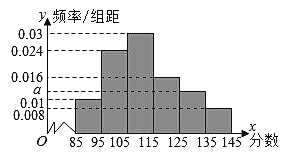
(1)求全市數學成績在135分以上的人數;
(2)試由樣本頻率分布直方圖佔計該校數學成績的平均分數;
(3)若從這50名學生中成績在125分(含125分)以上的同學中任意抽取3人,該3人在全市前13名的人數記為![]() ,求
,求![]() 的分布列和期望.
的分布列和期望.
附:若![]() ,則
,則![]() ,
,![]() ,
,
![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了解某市高三數學復習備考情況,該市教研機構組織了一次檢測考試,并隨機抽取了部分高三理科學生數學成績繪制如圖所示的頻率分布直方圖.

(1)根據頻率分布直方圖,估計該市此次檢測理科數學的平均成績![]() ;(精確到個位)
;(精確到個位)
(2)研究發現,本次檢測的理科數學成績![]() 近似服從正態分布
近似服從正態分布![]() (
(![]() ,
,![]() 約為
約為![]() ),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占
),按以往的統計數據,理科數學成績能達到自主招生分數要求的同學約占![]() .
.
(ⅰ)估計本次檢測成績達到自主招生分數要求的理科數學成績大約是多少分?(精確到個位)
(ⅱ)從該市高三理科學生中隨機抽取![]() 人,記理科數學成績能達到自主招生分數要求的人數為
人,記理科數學成績能達到自主招生分數要求的人數為![]() ,求
,求![]() 的分布列及數學期望
的分布列及數學期望![]() .(說明:
.(說明:![]() 表示
表示![]() 的概率.參考數據:
的概率.參考數據:![]() )
)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數,
為參數,![]() ),過點
),過點![]() 的直線
的直線![]() 的參數方程為
的參數方程為 (
(![]() 為參數).
為參數).
(Ⅰ)求曲線![]() 的普通方程,并說明它表示什么曲線;
的普通方程,并說明它表示什么曲線;
(Ⅱ)設曲線![]() 與直線
與直線![]() 分別交于
分別交于![]() ,
,![]() 兩點,若
兩點,若![]() ,
,![]() ,
,![]() 成等比數列,求
成等比數列,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“十二平均律”是通用的音律體系,明代朱載堉最早用數學方法計算出半音比例,為這個理論的發展做出了重要貢獻.十二平均律將一個純八度音程分成十二份,依次得到十三個單音,從第二個單音起,每一個單音的頻率與它的前一個單音的頻率的比都等于同一個常數.若第一個單音的頻率為f,第三個單音的頻率為![]() ,則第十個單音的頻率為( )
,則第十個單音的頻率為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設函數![]() ,則下列結論正確的是__________.(寫出所有正確的編號)①
,則下列結論正確的是__________.(寫出所有正確的編號)①![]() 的最小正周期為
的最小正周期為![]() ;②
;②![]() 在區間
在區間![]() 上單調遞增;③
上單調遞增;③![]() 取得最大值的
取得最大值的![]() 的集合為
的集合為![]() ④將
④將![]() 的圖像向左平移
的圖像向左平移![]() 個單位,得到一個奇函數的圖像
個單位,得到一個奇函數的圖像
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】射擊測試有兩種方案,方案1:先在甲靶射擊一次,以后都在乙靶射擊;方案2:始終在乙靶射擊,某射手命中甲靶的概率為![]() ,命中一次得3分;命中乙靶的概率為
,命中一次得3分;命中乙靶的概率為![]() ,命中一次得2分,若沒有命中則得0分,用隨機變量
,命中一次得2分,若沒有命中則得0分,用隨機變量![]() 表示該射手一次測試累計得分,如果
表示該射手一次測試累計得分,如果![]() 的值不低于3分就認為通過測試,立即停止射擊;否則繼續射擊,但一次測試最多打靶3次,每次射擊的結果相互獨立。
的值不低于3分就認為通過測試,立即停止射擊;否則繼續射擊,但一次測試最多打靶3次,每次射擊的結果相互獨立。
(1)如果該射手選擇方案1,求其測試結束后所得分![]() 的分布列和數學期望E
的分布列和數學期望E![]() ;
;
(2)該射手選擇哪種方案通過測試的可能性大?請說明理由。
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com