
在等比數列{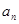 }中,
}中,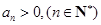 ,公比
,公比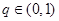 ,且
,且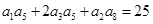 ,
, 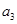 與
與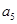 的等比中項為2.
的等比中項為2.
(1)求數列{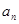 }的通項公式;
}的通項公式;
(2)設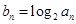 ,數列{
,數列{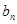 }的前
}的前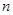 項和為
項和為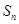 ,當
,當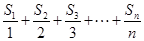 最大時,求
最大時,求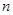 的值。
的值。
(1)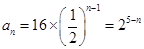
(2)n=8或9
【解析】解:(1)因為a1a5 + 2a3a5 +a 2a8=25,所以,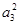 + 2a3a5 +
+ 2a3a5 +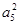 =25
=25
又an>o,…a3+a5=5,…………………………3分
又a3與a5的等比中項為2,所以,a3a5=4
而q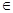 (0,1),所以,a3>a5,所以,a3=4,a5=1,
(0,1),所以,a3>a5,所以,a3=4,a5=1,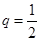 ,a1=16,所以,
,a1=16,所以,
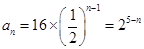 …………………………6分
…………………………6分
(2)bn=log2 an=5-n,所以,bn+1-bn=-1,
所以,{bn}是以4為首項,-1為公差的等差數列。。。。。。。。。8分
所以,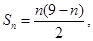
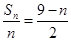 …………………………10分
…………………………10分
所以,當n≤8時,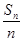 >0,當n=9時,
>0,當n=9時,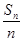 =0,n>9時,
=0,n>9時,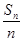 <0,
<0,
當n=8或9時,
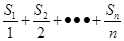 最大。 …………………………13分
最大。 …………………………13分


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:高中數學 來源:2010年北京東城區高三上學期理科數學綜合練習(一) 題型:解答題
在等比數列{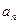 }中,
}中,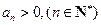 ,公比
,公比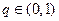 ,且
,且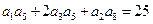 ,
, 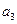 與
與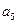 的等比中項為2.
的等比中項為2.
(1)求數列{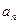 }的通項公式;
}的通項公式;
(2)設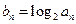 ,數列{
,數列{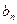 }的前
}的前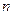 項和為
項和為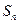 ,當
,當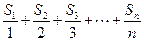 最大時,求
最大時,求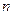 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com