
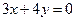 �����^�c
�����^�c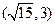 ���p�����Ę�(bi��o)��(zh��n)���̣�������p�������x����.
���p�����Ę�(bi��o)��(zh��n)���̣�������p�������x����. ��У�n��ϵ�д�
��У�n��ϵ�д�
| �꼉 | �����n�� | �꼉 | �����n�� |
| ��һ | ��һ���M�n�����]�� | ��һ | ��һ���M�n�����]�� |
| �߶� | �߶����M�n�����]�� | ���� | �������M�n�����]�� |
| ���� | �������M�n�����]�� | ���� | �������M�n�����]�� |
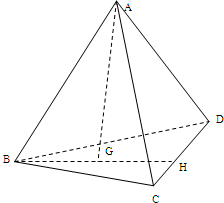
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
| AB |
| AC |
| AD |
| AG |
| AB |
| AC |
| AD |
| AG |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
| A��1�� | B��2�� | C��3�� | D��4�� |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
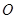 ��O�c��
��O�c��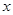 �S�������S��O�S����֪�c
�S�������S��O�S����֪�c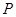 ��ֱ������(bi��o)��
��ֱ������(bi��o)��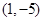 ���c
���c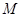 �ĘO����(bi��o)��
�ĘO����(bi��o)��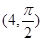 ����ֱ��
����ֱ��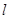 �^�c
�^�c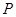 ���҃Aб�Ǟ�
���҃Aб�Ǟ�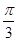 ���A
���A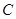 ��
��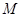 �� �A�ġ�
�� �A�ġ�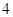 ��돽��
��돽��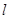 �ą���(sh��)���̺͈A
�ą���(sh��)���̺͈A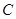 �ĘO����(bi��o)���̣�
�ĘO����(bi��o)���̣�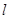 �͈A
�͈A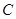 ��λ���P(gu��n)ϵ��
��λ���P(gu��n)ϵ���鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
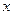 �S�ϣ�����һ����c��
�S�ϣ�����һ����c��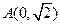 �����x���ʵ���
�����x���ʵ���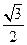 ���^�c
���^�c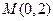 ��ֱ��
��ֱ��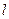 �c�E�A�ཻ�ڲ�ͬ���c
�c�E�A�ཻ�ڲ�ͬ���c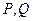 ���c
���c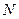 �ھ���
�ھ���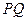 �ϡ�
�ϡ�
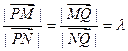 ����ֱ��
����ֱ��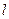 �c
�c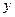 �S���غϣ�
�S���غϣ�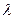 ��ȡֵ������
��ȡֵ�������鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
 ��
��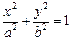 ��
��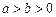 ���������ҽ��c�քe��
���������ҽ��c�քe��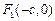 ��
��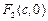 ����
����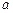 ��
��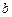 ��
�� �ɵȱȔ�(sh��)�У�
�ɵȱȔ�(sh��)�У�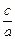 ��ֵ��
��ֵ�� ������c������c�քe��
������c������c�քe��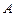 ��
��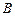 �����C��
�����C��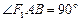 ��
��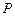 ��E�A
��E�A �ϵ�����һ�c���Ƿ�����^�c
�ϵ�����һ�c���Ƿ�����^�c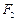 ��
��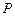 ��ֱ��
��ֱ�� ��ʹ
��ʹ �c
�c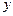 �S�Ľ��c
�S�Ľ��c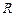 �M��
�M��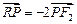 �������ڣ���ֱ��
�������ڣ���ֱ�� ��б��
��б��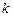 ���������ڣ�Ո�f�����ɣ�
���������ڣ�Ո�f�����ɣ��鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ����x�}
 ����A��B���c���^ԭ�c�c����AB���c�B����б�ʞ�
����A��B���c���^ԭ�c�c����AB���c�B����б�ʞ�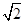 ���t
���t ��ֵ����( )
��ֵ����( ) 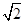 B��
B��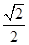 C��
C�� D��
D��
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��Դ����Ԕ �}�ͣ�����}
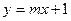 �c�p����
�c�p����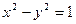 �Ѓɂ���ͬ�Ĺ����c���t����(sh��)
�Ѓɂ���ͬ�Ĺ����c���t����(sh��)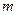 ��ȡֵ������
��ȡֵ������ �鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)���б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��ƽ�_ | �W(w��ng)���к���Ϣ�e�^(q��) | ����p�_�e�^(q��) | ��vʷ̓�o���x�к���Ϣ�e�^(q��) | �����֙�(qu��n)�e�^(q��)
�`���Ͳ�����Ϣ�e���Ԓ��027-86699610 �e���]�䣺58377363@163.com