
【題目】某印刷廠為了研究印刷單冊書籍的成本y(單位:元)與印刷冊數x(單位:千冊)之間的關系,在印制某種書籍時進行了統計,相關數據見下表:

根據以上數據,技術人員分別借助甲、乙兩種不同的回歸模型,得到了兩個回歸方程,甲: ![]()
為了評價兩種模型的擬合效果,完成以下任務:
(1)(ⅰ)完成下表(計算結果精確到0.1):
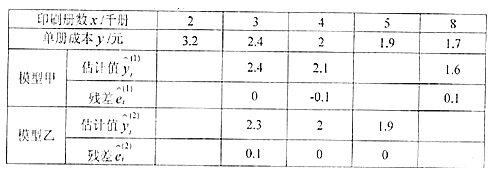
(ⅱ)分別計算模型甲與模型乙的殘差平方和![]() 及
及![]() ,并通過比較
,并通過比較![]() ,
,![]() 的大小,判斷哪個模型擬合效果更好.
的大小,判斷哪個模型擬合效果更好.
(2)該書上市后,受到廣大讀者的熱烈歡迎,不久便全部售罄,于是印刷廠決定進行二次印刷,根據市場調查,新需求量為8千冊(概率為0.8)或10千冊(概率為0.2),若印刷廠以沒測5元的價格將書籍出售給訂貨商,問印刷廠二次印刷8千冊還是10千冊恒獲得更多的利潤?(按(1)中擬合效果較好的模型計算印刷單冊書的成本)
【答案】(1)(ⅰ)見解析(ⅱ)模型乙的擬合效果更好.(2)印刷8千冊對印刷廠更有利.
【解析】試題分析:(1)(ⅰ)根據公式計算,填入對應表格(ⅱ) 比較殘差平方和大小,越小越好,故模型乙的擬合效果更好.(2)分別計算印刷8千冊與10千冊的利潤:二次印刷8千冊,則印刷廠獲利為![]() (元),如二次印刷10千冊,則每冊成本為
(元),如二次印刷10千冊,則每冊成本為![]() ,需求期望值為
,需求期望值為![]() .因而獲利為
.因而獲利為![]() ,少于印刷8千冊獲的利潤.
,少于印刷8千冊獲的利潤.
試題解析:解:(Ⅰ) (ⅰ) 經計算,可得下表.
印刷冊數 | 2 | 3 | 4 | 5 | 8 | |
單冊成本 | 3.2 | 2.4 | 2 | 1.9 | 1.7 | |
模型甲 | 估計值 | 3.1 | 2.4 | 2.1 | 1.9 | 1.6 |
殘差 | 0.1 | 0 | -0.1 | 0 | 0.1 | |
模型乙 | 估計值 | 3.2 | 2.3 | 2 | 1.9 | 1.7 |
殘差 | 0 | 0.1 | 0 | 0 | 0 | |
(ⅱ) ![]() ,
, ![]() ,
,
![]() ,故模型乙的擬合效果更好.
,故模型乙的擬合效果更好.
(Ⅱ) 若二次印刷8千冊,則印刷廠獲利為![]() (元) .
(元) .
若二次印刷10千冊,由(Ⅰ)可知,單冊書印刷成本為![]() (元),
(元),
故印刷總成本為![]() (元) .
(元) .
設新需求量為![]() (千冊),印刷廠利潤為
(千冊),印刷廠利潤為![]() (元),則
(元),則
| 8 | 10 |
| 0.8 | 0.2 |
![]() .
.
故![]() .
.
故印刷8千冊對印刷廠更有利.


 七彩題卡口算應用一點通系列答案
七彩題卡口算應用一點通系列答案科目:高中數學 來源: 題型:
【題目】已知直線![]() ,半徑為
,半徑為![]() 的圓
的圓![]() 與
與![]() 相切,圓心
相切,圓心![]() 在
在![]() 軸上且在直線
軸上且在直線![]() 的上方.
的上方.
(Ⅰ)求圓![]() 的標準方程;
的標準方程;
(Ⅱ)過點![]() 的直線與圓
的直線與圓![]() 交于
交于![]() 兩點(
兩點(![]() 在
在![]() 軸上方),問在
軸上方),問在![]() 軸正半軸上是否存在點
軸正半軸上是否存在點![]() ,使得
,使得![]() 軸平分
軸平分![]() ?若存在,請求出點
?若存在,請求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】小王創建了一個由他和甲、乙、丙共4人組成的微信群,并向該群發紅包,每次發紅包的個數為1個(小王自己不搶),假設甲、乙、丙3人每次搶得紅包的概率相同.
(Ⅰ)若小王發2次紅包,求甲恰有1次搶得紅包的概率;
(Ⅱ)若小王發3次紅包,其中第1,2次,每次發5元的紅包,第3次發10元的紅包,記乙搶得所有紅包的錢數之和為X,求X的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知空間四邊形ABCD的兩條對角線的長AC=6,BD=8,AC與BD所成的角為30o , E,F,G,H分別是AB,BC,CD,DA的中點,求四邊形EFGH的面積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知過原點的動直線l與圓C1:x2+y2﹣6x+5=0相交于不同的兩點A,B.
(1)求圓C1的圓心坐標;
(2)求線段AB 的中點M的軌跡C的方程;
(3)是否存在實數 k,使得直線L:y=k(x﹣4)與曲線 C只有一個交點?若存在,求出k的取值范圍;若不存在,說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】某單位有老年人30人,中年人90人,青年人60人,為了調查他們的身體健康狀況,采用分層抽樣的方法從他們中間抽取一個容量為36的樣本,則應抽取老年人的人數是( )
A.5
B.6
C.7
D.8
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com