Question

【題目】已知奇函數f（x）= 的定義域為[﹣a﹣2，b]
（1）求實數a，b的值；
（2）判斷函數f（x）的單調性，并用定義給出證明；
（3）若實數m滿足f（m﹣1）＜f（1﹣2m），求m的取值范圍．

Answer 1

【答案】
（1）∵f（x）是奇函數，故f（0）=0，

即a﹣1=0，解得：a=1，故﹣a﹣2=﹣3，

定義域為[﹣a﹣2，b]，關于原點對稱，

故b=3

（2）函數f（x）在[﹣3，3]遞增，

證明如下：設x1，x2是[﹣3，3]上的任意2個值，且x1＜x2，

則f（x1）﹣f（x2）= ﹣ = ，

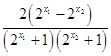∵﹣3≤x1＜x2≤3，∴ ﹣ ＜0，又 +1＞0， +1＞0，

∴f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），

∴f（x）在[﹣3，3]遞增

（3）由（1）得f（x）在[﹣3，3]遞增，

∴f（m﹣1）＜f（1﹣2m）等價于：

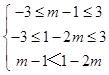，解得：﹣1≤m＜ ，

故不等式的解集是[﹣1， ）

【解析】（1）根據函數的奇偶性求出a，b的值即可；（2）根據函數單調性的定義證明即可；（3）根據函數的單調性以及函數的定義域得到關于m的不等式組，解出即可．
【考點精析】通過靈活運用函數單調性的判斷方法和函數奇偶性的性質，掌握單調性的判定法：①設x1,x2是所研究區間內任兩個自變量，且x1＜x2；②判定f(x1)與f(x2)的大小；③作差比較或作商比較；在公共定義域內，偶函數的加減乘除仍為偶函數；奇函數的加減仍為奇函數；奇數個奇函數的乘除認為奇函數；偶數個奇函數的乘除為偶函數；一奇一偶的乘積是奇函數;復合函數的奇偶性：一個為偶就為偶，兩個為奇才為奇即可以解答此題．