
【題目】如圖,在四棱錐中![]() ,底面
,底面![]() 為邊長為
為邊長為![]() 的正方形,
的正方形, ![]() ,
, ![]() 分別為
分別為![]() ,
, ![]() 的中點.
的中點.
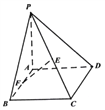
(1)求證: ![]()
![]() 平面
平面![]() ;
;
(2)若![]() ,
, ![]() 平面
平面![]() ,求直線
,求直線![]() 與平面
與平面![]() 所成角的大小.
所成角的大小.
【答案】(1)見解析;(2)![]() .
.
【解析】試題分析:(1)設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
, ![]() ,根據三角形中位線定理可得
,根據三角形中位線定理可得![]() ,進而得四邊形
,進而得四邊形![]() 為平行四邊形,從而
為平行四邊形,從而![]() ,由線面平行的判定定理可得
,由線面平行的判定定理可得![]()
![]() 平面
平面![]() ;(2)由(1)知,
;(2)由(1)知, ![]() ,因為
,因為![]() 平面
平面![]() ,可得
,可得![]() 平面
平面![]() ,
, ![]() ,可證明
,可證明![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,向量
為坐標原點,向量![]() ,
, ![]() ,
, ![]() 的方向為
的方向為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸的正方形建立如圖所示的空間直角坐標系
軸的正方形建立如圖所示的空間直角坐標系![]() ,求出直線
,求出直線![]() 的方向向量與平面
的方向向量與平面![]() 的法向量,利用空間向量夾角余弦公式可得直線
的法向量,利用空間向量夾角余弦公式可得直線![]() 與平面
與平面![]() 所成角的正弦值,從而可得結果.
所成角的正弦值,從而可得結果.
試題解析:(1)設![]() 的中點為
的中點為![]() ,連接
,連接![]() ,
, ![]() ,
,
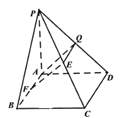
則![]() ,而
,而![]()
∴![]() ∴四邊形
∴四邊形![]() 為平行四邊形.
為平行四邊形.
∴![]() ,而
,而![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() 平面
平面![]() ;
;
(2)由(1)知, ![]() ,因為
,因為![]() 平面
平面![]()
所以![]() 平面
平面![]() ,而
,而![]() ,
, ![]()
![]() 平面
平面![]()
∴![]()
∵![]() ,
, ![]() ,
, ![]()
∴![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
∴![]() ,而
,而![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]()
(注意:沒有證明出![]() 平面
平面![]() ,直接運用這一結論的,后續過程不給分)
,直接運用這一結論的,后續過程不給分)
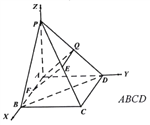
由題意, ![]() ,
, ![]() ,
, ![]() 兩兩垂直,以
兩兩垂直,以![]() 為坐標原點,向量
為坐標原點,向量![]() ,
, ![]() ,
, ![]() 的方向為
的方向為![]() 軸,
軸, ![]() 軸,
軸, ![]() 軸的正方形建立如圖所示的空間直角坐標系
軸的正方形建立如圖所示的空間直角坐標系![]()
在三角形![]() 中
中![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,知
,知![]() ,而
,而![]() 的中點為
的中點為![]() 知
知![]() ,則
,則![]() ,
, ![]() ,
, 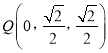 ,
, ![]() ,
, ![]()
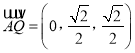 ,
, ![]() ,
, ![]() 為平面
為平面![]() 的一個法向量.
的一個法向量.
設直線![]() 與平面
與平面![]() 所成角為
所成角為![]() ,
, 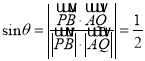
所以直線![]() 與平面
與平面![]() 所成角為
所成角為![]() .
.
【方法點晴】本題主要考查線面平行的判定定理、直線和平面成的角的定義及求法,屬于難題.證明線面平行的常用方法:①利用線面平行的判定定理,使用這個定理的關鍵是設法在平面內找到一條與已知直線平行的直線,可利用幾何體的特征,合理利用中位線定理、線面平行的性質或者構造平行四邊形、尋找比例式證明兩直線平行.②利用面面平行的性質,即兩平面平行,在其中一平面內的直線平行于另一平面. 本題(1)是就是利用方法①證明的.


科目:高中數學 來源: 題型:
【題目】半期考試后,班長小王統計了50名同學的數學成績,繪制頻率分布直方圖如圖所示.

(1)根據頻率分布直方圖,估計這50名同學的數學成績的眾數;
(2)用分層抽樣的方法從成績低于115的同學中抽取6名,再在抽取的這6名同學中任選2名,求這兩名同學數學成績均在![]() 中的概率.
中的概率.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,且
,且![]() .
.
(1)求實數![]() 的值,并指出函數
的值,并指出函數![]() 的定義域;
的定義域;
(2)將函數![]() 圖象上的所有點向右平行移動1個單位得到函數
圖象上的所有點向右平行移動1個單位得到函數![]() 的圖象,寫出函數
的圖象,寫出函數![]() 的表達式;
的表達式;
(3)對于(2)中的![]() ,關于
,關于![]() 的函數
的函數![]() 在
在![]() 上的最小值為2,求
上的最小值為2,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】在直角坐標平面內,以坐標原點![]() 為極點,
為極點, ![]() 軸的非負半軸為極軸建立極坐標系.已知點
軸的非負半軸為極軸建立極坐標系.已知點![]() 、
、![]() 的極坐標分別為
的極坐標分別為![]() 、
、![]() ,曲線
,曲線![]() 的參數方程為
的參數方程為![]() (
(![]() 為參數).
為參數).
(1)求直線![]() 的直角坐標方程;
的直角坐標方程;
(2)若直線![]() 和曲線
和曲線![]() 只有一個交點,求
只有一個交點,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】【2018衡水金卷(二)】如圖,矩形![]() 中,
中, ![]() 且
且![]() ,
, ![]() 交
交![]() 于點
于點![]() .
.
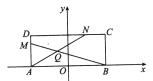
(I)若點![]() 的軌跡是曲線
的軌跡是曲線![]() 的一部分,曲線
的一部分,曲線![]() 關于
關于![]() 軸、
軸、![]() 軸、原點都對稱,求曲線
軸、原點都對稱,求曲線![]() 的軌跡方程;
的軌跡方程;
(II)過點![]() 作曲線
作曲線![]() 的兩條互相垂直的弦
的兩條互相垂直的弦![]() ,四邊形
,四邊形![]() 的面積為
的面積為![]() ,探究
,探究![]() 是否為定值?若是,求出此定值,若不是,請說明理由.
是否為定值?若是,求出此定值,若不是,請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com