
已知各項(xiàng)均不相等的等差數(shù)列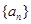 的前三項(xiàng)和為18,
的前三項(xiàng)和為18,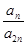 是一個(gè)與
是一個(gè)與 無(wú)關(guān)的常數(shù),若
無(wú)關(guān)的常數(shù),若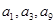 恰為等比數(shù)列
恰為等比數(shù)列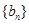 的前三項(xiàng),(1)求
的前三項(xiàng),(1)求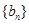 的通項(xiàng)公式.(2)記數(shù)列
的通項(xiàng)公式.(2)記數(shù)列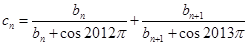 ,
,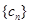 的前三
的前三 項(xiàng)和為
項(xiàng)和為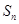 ,求證:
,求證: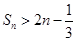
(1) ;(2)先求和,然后再利用放縮法證明
;(2)先求和,然后再利用放縮法證明
解析試題分析:(1)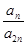 是一個(gè)與
是一個(gè)與 無(wú)關(guān)的常數(shù)
無(wú)關(guān)的常數(shù) ………2分
………2分
又

 ………4分
………4分 ………6分
………6分
(2) …8分
…8分
又因?yàn)?img src="http://thumb.zyjl.cn/pic5/tikupic/48/c/1w5rt3.png" style="vertical-align:middle;" />
即 ……12分
……12分
所以: ……12分
……12分
考點(diǎn):本題考查了數(shù)列的通項(xiàng)和前n項(xiàng)和公式
點(diǎn)評(píng):數(shù)列的通項(xiàng)公式及應(yīng)用是數(shù)列的重點(diǎn)內(nèi)容,數(shù)列的大題對(duì)邏輯推理能力有較高的要求,在數(shù)列中突出考查學(xué)生的理性思維,這是近幾年新課標(biāo)高考對(duì)數(shù)列考查的一個(gè)亮點(diǎn),也是一種趨勢(shì).隨著新課標(biāo)實(shí)施的深入,高考關(guān)注的重點(diǎn)為等差、等比數(shù)列的通項(xiàng)公式,錯(cuò)位相減法、裂項(xiàng)相消法等求數(shù)列的前n項(xiàng)的和等等


 學(xué)練快車(chē)道快樂(lè)假期暑假作業(yè)新疆人民出版社系列答案
學(xué)練快車(chē)道快樂(lè)假期暑假作業(yè)新疆人民出版社系列答案 浙大優(yōu)學(xué)小學(xué)年級(jí)銜接導(dǎo)與練浙江大學(xué)出版社系列答案
浙大優(yōu)學(xué)小學(xué)年級(jí)銜接導(dǎo)與練浙江大學(xué)出版社系列答案 小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案
小學(xué)暑假作業(yè)東南大學(xué)出版社系列答案 津橋教育暑假拔高銜接廣東人民出版社系列答案
津橋教育暑假拔高銜接廣東人民出版社系列答案 波波熊暑假作業(yè)江西人民出版社系列答案
波波熊暑假作業(yè)江西人民出版社系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知等差數(shù)列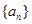 的前
的前 項(xiàng)和為
項(xiàng)和為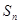 ,且
,且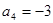 ,
,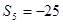
(1)求數(shù)列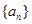 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)求數(shù)列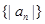 的前
的前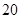 項(xiàng)和
項(xiàng)和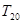 .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列 :
:
(1)觀察規(guī)律,寫(xiě)出數(shù)列 的通項(xiàng)公式,它是個(gè)什么數(shù)列?
的通項(xiàng)公式,它是個(gè)什么數(shù)列?
(2)若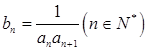 ,設(shè)
,設(shè) ,求
,求 。
。
(3)設(shè)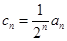 ,
, 為數(shù)列
為數(shù)列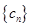 的前
的前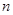 項(xiàng)和,求
項(xiàng)和,求 。
。
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知數(shù)列 中,
中, ,前
,前 項(xiàng)的和為
項(xiàng)的和為 ,對(duì)任意的
,對(duì)任意的 ,
, ,
, ,
, 總成等差數(shù)列.
總成等差數(shù)列.
(1)求 的值;
的值;
(2)求通項(xiàng) ;
;
(3)證明: .
.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
各項(xiàng)均為正數(shù)的數(shù)列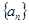 前
前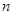 項(xiàng)和為
項(xiàng)和為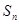 ,且
,且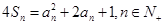 .
.
(1)求數(shù)列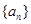 的通項(xiàng)公式;
的通項(xiàng)公式;
(2)已知公比為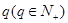 的等比數(shù)列
的等比數(shù)列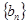 滿足
滿足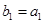 ,且存在
,且存在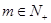 滿足
滿足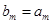 ,
,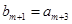 ,求數(shù)列
,求數(shù)列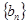 的通項(xiàng)公式.
的通項(xiàng)公式.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
已知等差數(shù)列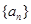 滿足
滿足 ,
,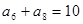
(I) 求數(shù)列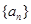 的通項(xiàng)公式;
的通項(xiàng)公式;
(II) 求數(shù)列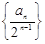 的前n項(xiàng)和.
的前n項(xiàng)和.
查看答案和解析>>
科目:高中數(shù)學(xué) 來(lái)源: 題型:解答題
(本小題滿分12分)在數(shù)列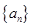 中,
中,  ,
, ,
, .
.
(Ⅰ)證明數(shù)列 是等比數(shù)列;
是等比數(shù)列;
(II)求數(shù)列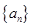 的前
的前 項(xiàng)和
項(xiàng)和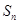 .
.
(Ⅲ)證明對(duì)任意 ,不等式
,不等式 成立.
成立.
查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專(zhuān)區(qū) | 電信詐騙舉報(bào)專(zhuān)區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專(zhuān)區(qū) | 涉企侵權(quán)舉報(bào)專(zhuān)區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com