
 x2-x+
x2-x+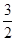 是[1,b]上的“四維光軍”函數,求常數b的值;
是[1,b]上的“四維光軍”函數,求常數b的值; 是區間[a,b]上的“四維光軍”函數?若存在,求出a,b的值,否則,請說明理由.
是區間[a,b]上的“四維光軍”函數?若存在,求出a,b的值,否則,請說明理由. 寒假天地重慶出版社系列答案
寒假天地重慶出版社系列答案科目:高中數學 來源:不詳 題型:單選題

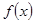 =x
=x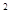 +2(a-1)x+2在區間(-∞,4)上是減函數,則實數a的取值范圍是( )。
+2(a-1)x+2在區間(-∞,4)上是減函數,則實數a的取值范圍是( )。| A.a≥-3 | B. a≤-3 | C. a≤5 | D. a≥3 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com