
低碳生活,從“衣食住行”開始.在國內一些網站中出現了“碳足跡”的應用,人們可以由此計算出自己每天的碳排放量,如家居用電的二氧化碳排放量(千克)=耗電度數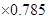 ,家用天然氣的二氧化碳排放量(千克)=天然氣使用立方數
,家用天然氣的二氧化碳排放量(千克)=天然氣使用立方數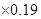 等.某校開展“節能減排,保護環境,從我做起!”的活動,該校高一、六班同學利用假期在東城、西城兩個小區進行了逐戶的關于“生活習慣是否符合低碳排放標準”的調查.生活習慣符合低碳觀念的稱為“低碳家庭”,否則稱為“非低碳家庭”.經統計,這兩類家庭占各自小區總戶數的比例
等.某校開展“節能減排,保護環境,從我做起!”的活動,該校高一、六班同學利用假期在東城、西城兩個小區進行了逐戶的關于“生活習慣是否符合低碳排放標準”的調查.生活習慣符合低碳觀念的稱為“低碳家庭”,否則稱為“非低碳家庭”.經統計,這兩類家庭占各自小區總戶數的比例 數據如下:
數據如下:
(1)如果在東城、西城兩個小區內各隨機選擇2個家庭,求這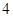 個家庭中恰好有兩個家庭是“低碳家庭”的概率;
個家庭中恰好有兩個家庭是“低碳家庭”的概率;
(2)該班同學在東城小區經過大力宣傳節能減排的重要意義,每周“非低碳家庭”中有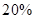 的家庭能加入到“低碳家庭”的行列中.宣傳兩周后隨機地從東城小區中任選
的家庭能加入到“低碳家庭”的行列中.宣傳兩周后隨機地從東城小區中任選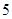 個家庭,記
個家庭,記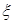 表示
表示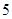 個家庭中“低碳家庭”的個數,求
個家庭中“低碳家庭”的個數,求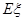 和
和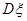 .
.
(1)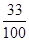 ;(2)
;(2)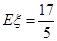 ,
,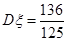 .
.
解析試題分析:本題主要考查獨立性事件、二項分布、隨機變量的分布列、數學期望和方差等基礎知識,考查學生的分析問題解決問題的能力、計算能力.第一問,4個家庭中恰好有一個兩個家庭是“低碳家庭”,分三種情況討論:“低碳家庭”均來自東城小區,“低碳家庭”分別來自東城、西城兩個小區,“低碳家庭”均來自西城小區,每種情況都是四個家庭的概率相乘;第二問,東城小區每周有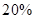 的人加入“低碳家庭”行列,經過兩周后,非低碳家庭占東城小區總家庭數的比例為
的人加入“低碳家庭”行列,經過兩周后,非低碳家庭占東城小區總家庭數的比例為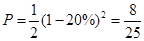 ,得到A小區低碳家庭和非低碳家庭的概率,由題意分析,隨機變量
,得到A小區低碳家庭和非低碳家庭的概率,由題意分析,隨機變量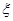 服從二項分布,利用二項分布的期望、方差的計算公式計算.
服從二項分布,利用二項分布的期望、方差的計算公式計算.
試題解析:(1)設事件“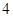 個家庭中恰好有兩個家庭是‘低碳家庭’”為
個家庭中恰好有兩個家庭是‘低碳家庭’”為 , 1分
, 1分
則有以下三種情況:“低碳家庭”均來自東城小區,“低碳家庭”分別來自東城、西城兩個小區,“低碳家庭”均來自西城小區.
∴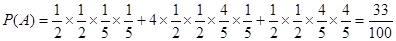 .6分
.6分
(2)因為東城小區每周有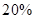 的人加入“低碳家庭”行列,經過兩周后,兩類家庭占東城小區總家庭數的比例如下:
的人加入“低碳家庭”行列,經過兩周后,兩類家庭占東城小區總家庭數的比例如下:
8分 小區
小區低碳家庭 非低碳家庭 
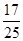
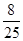
由題意,兩周后東城小區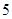 個家庭中的“低碳家庭”的個數
個家庭中的“低碳家庭”的個數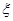 服從二項分布,
服從二項分布,
即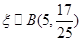 10分
10分
∴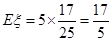 , 11分
, 11分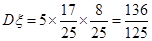 . 12分
. 12分
考點:獨立性事件、二項分布、隨機變量的分布列、數學期望和方差.


 閱讀快車系列答案
閱讀快車系列答案科目:高中數學 來源: 題型:解答題
袋中裝有大小和形狀相同的小球若干個黑球和白球,且黑球和白球的個數比為4:3,從中任取2個球都是白球的概率為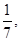 現不放回從袋中摸取球,每次摸一球,直到取到白球時即終止,每個球在每一次被取出的機會是等可能的,用
現不放回從袋中摸取球,每次摸一球,直到取到白球時即終止,每個球在每一次被取出的機會是等可能的,用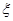 表示取球終止時所需要的取球次數.
表示取球終止時所需要的取球次數.
(1)求袋中原有白球、黑球的個數;
(2)求隨機變量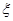 的分布列和數學期望.
的分布列和數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
如圖,A地到火車站共有兩條路徑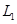 和
和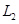 ,據統計,通過兩條路徑所用的時間互不影響,所用時間落在個時間段內的頻率如下表:
,據統計,通過兩條路徑所用的時間互不影響,所用時間落在個時間段內的頻率如下表:
| 時間(分鐘) | 10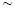 20 20 | 20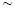 30 30 | 30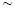 40 40 | 40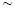 50 50 | 50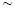 60 60 |
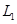 的頻率 的頻率 | 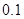 | 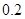 | 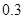 | 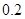 | 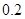 |
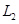 的頻率 的頻率 | 0 | 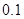 | 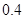 | 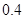 | 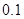 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
先后拋擲一枚骰子,得到的點數分別記為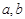 ,按以下程序進行運算:
,按以下程序進行運算:
(1)若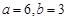 ,求程序運行后計算機輸出的y的值;
,求程序運行后計算機輸出的y的值;
(2)若“輸出y的值是3”為事件A,求事件A發生的概率.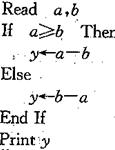
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
設進入某商場的每一位顧客購買甲種商品的概率為0.5,購買乙種商品的概率為0.6,且購買甲種商品與購買乙種商品相互獨立,各顧客之間購買商品也是相互獨立的.
(1)求進入商場的1位顧客購買甲、乙兩種商品中的一種的概率;
(2)求進入商場的1位顧客至少購買甲、乙兩種商品中的一種的概率;
(3)記ξ表示進入商場的3位顧客中至少購買甲、乙兩種商品中的一種的人數,求ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
一批產品需要進行質量檢驗,檢驗方案是:先從這批產品中任取4件作檢驗,這4件產品中優質品的件數記為n.如果n=3,再從這批產品中任取4件作檢驗,若都為優質品,則這批產品通過檢驗;如果n=4,再從這批產品中任取1件作檢驗,若為優質品,則這批產品通過檢驗;其他情況下,這批產品都不能通過檢驗.
假設這批產品的優質品率為50%,即取出的產品是優質品的概率都為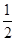 ,且各件產品是否為優質品相互獨立.
,且各件產品是否為優質品相互獨立.
(1)求這批產品通過檢驗的概率;
(2)已知每件產品檢驗費用為100元,凡抽取的每件產品都需要檢驗,對這批產品作質量檢驗所需的費用記為X(單位:元),求X的分布列及數學期望.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
已知甲盒內有大小相同的1個紅球和3個黑球,乙盒內有大小相同的2個紅球和4個黑球.現從甲、乙兩個盒內各任取2個球.
(1)求取出的4個球均為黑球的概率;
(2)求取出的4個球中恰有1個紅球的概率;
(3)設ξ為取出的4個球中紅球的個數,求ξ的分布列.
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
年齡在60歲(含60歲)以上的人稱為老齡人,某地區老齡人共有35萬,隨機調查了該地區700名老齡人的健康狀況,結果如下表:
| 健康指數 | 2 | 1 | 0 | -1 |
| 60歲至79歲的人數 | 250 | 260 | 65 | 25 |
| 80歲及以上的人數 | 20 | 45 | 20 | 15 |
查看答案和解析>>
科目:高中數學 來源: 題型:解答題
某工藝廠開發一種新工藝品,頭兩天試制中,該廠要求每位師傅每天制作10件,該廠質檢部每天從每位師傅制作的10件產品中隨機抽取4件進行檢查,若發現有次品,則當天該師傅的產品不能通過.已知李師傅第一天、第二天制作的工藝品中分別有2件、1件次品.
(1)求兩天中李師傅的產品全部通過檢查的概率;
(2)若廠內對師傅們制作的工藝品采用記分制,兩天全不通過檢查得0分,通過1天、2天分別得1分、2分,求李師傅在這兩天內得分的數學期望.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com