求經過點A(-2,-1),B(6,-5),且圓心在直線x+y-2=0上的圓的方程.
【答案】
分析:求出線段AB的中點M的坐標和線段AB的斜率,即得AB的中垂線的斜率,用點斜式求AB的中垂線的方程,將此方程與
直線x+y-2=0 聯立方程組,求得圓心的坐標,利用兩點間的距離公式求得半徑,即可求出圓的標準方程.
解答:解:線段AB中點M的坐標為(2,-3),K
AB=
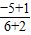
=-

,
故線段AB的中垂線的方程為 y+3=2(x-2),即 y=2x-7,
于是,解方程組
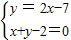
求得圓心坐標為(3,-1),
故圓的半徑 r
2=(6-3)
2+(-5+1)
2=25,所以所求圓的方程為 (x-3)
2+(y+1)
2=25.
點評:本題考查用點斜式求直線的方程,求圓的標準方程的方法,求出圓心坐標和半徑的值,是解題的關鍵.

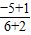 =-
=- ,
,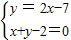 求得圓心坐標為(3,-1),
求得圓心坐標為(3,-1),

 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案