
| A、1:1 | B、1:2 | C、1:8 | D、1:7 |
| V柱 |
| V錐 |
| πxy2 | ||
|
| 3xy2 |
| nm2 |
| y |
| m |
| n-x |
| n |
| 6x |
| πnm |
| x |
| n |
| n |
| 2 |


 期末1卷素質教育評估卷系列答案
期末1卷素質教育評估卷系列答案科目:高中數學 來源: 題型:044
如圖所示,已知圓錐的底面半徑為R,高為H,在其中有一個高為x,下底面半徑與上底面半徑之比為λ(0<λ<1)的內接圓臺.試問:當x為何值時,圓臺的體積最大?并求出這個最大的體積.
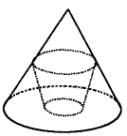
查看答案和解析>>
科目:高中數學 來源:數學教研室 題型:044

查看答案和解析>>
科目:高中數學 來源:2010年高三備考數學好題系列(04)(解析版) 題型:選擇題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com