
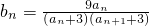 ,記數列{bn}的前n項和為Tn,證明對于任意的正整數n,都有
,記數列{bn}的前n項和為Tn,證明對于任意的正整數n,都有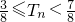 成立.
成立.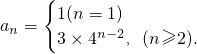
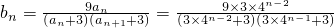 =
=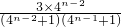 ,
,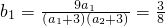 ,
,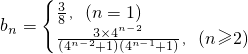 .
. 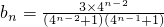 =
=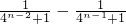
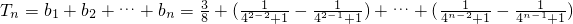
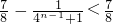 .
. 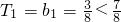
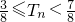 成立.
成立.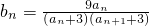 得bn的通項公式求出Tn,利用其單調性與放縮法證明不等式
得bn的通項公式求出Tn,利用其單調性與放縮法證明不等式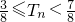 .
.

 學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案
學期復習一本通學習總動員期末加暑假延邊人民出版社系列答案 芒果教輔暑假天地重慶出版社系列答案
芒果教輔暑假天地重慶出版社系列答案科目:高中數學 來源: 題型:
| n+1 |
| 2 |
| 2n |
| an |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com