設函數f(x)=|x|x+bx+c,則下列命題中正確命題的序號有 (請將你認為正確命題的序號都填上)
①當b>0時,函數f(x)在R上是單調增函數;
②當b<0時,函數f(x)在R上有最小值;
③函數f(x)的圖象關于點(0,c)對稱;
④方程f(x)=0可能有三個實數根.
【答案】
分析:①當b>0時,把函數f(x)=|x|x+bx+c分x≥0和x<0兩種情況討論,轉化為二次函數求單調性;
②當b<0時,函數f(x)在R上有最小值,可以根據函數的對稱性加以判斷;
③函數f(x)的圖象關于點(0,c)對稱,可以根據函數圖象的平移解決;
④方程f(x)=0可能有三個實數根,對b,c去特殊值.
解答:解:①當b>0時,f(x)=|x|x+bx+c=
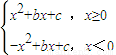
,知函數f(x)在R上是單調增函數;
②當b<0時,f(x)=|x|x+bx+c=
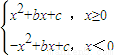
值域是R,故函數f(x)在R上沒有最小值;
③若f(x)=|x|x+bx那么函數f(x)是奇函數(f(-x)=-f(x)),也就是說函數f(x)的圖象關于(0,0)對稱.而函數f(x)=|x|x+bx+c的圖象是由函數f(x)=|x|x+bx的圖象沿Y軸移動,故圖象一定是關于(0,c)對稱的.
④令b=-2,c=0,則f(x)=|x|x-2x=0,解得x=0,2,-2.所以正確.
故答案為:①③④.
點評:此題考查了分段函數的單調性、對稱性和最值問題,對于含有絕對值的一類問題,通常采取去絕對值的方法解決,體現了分類討論的數學思想;函數的對稱性問題一般轉化為函數的奇偶性加以分析,再根據函數圖象的平移解決,體現了轉化、運動的數學思想;對于存在性的命題研究,一般通過特殊值法來解決.是好題,屬中檔題.

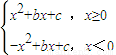 ,知函數f(x)在R上是單調增函數;
,知函數f(x)在R上是單調增函數;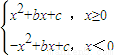 值域是R,故函數f(x)在R上沒有最小值;
值域是R,故函數f(x)在R上沒有最小值;
