【答案】
分析:方程的左邊對應一個函數,作出它的圖象是位于x軸上方的曲線,由拋物線y=x
2-5x+4變換而來,而方程的右邊對應一條經過點(2.5,0)的直線,討論斜率k的正負,觀察兩個圖象的交點個數,不難選出正確答案.
解答: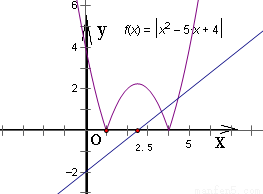
解:記f(x)=|x
2-5x+4|,作出它的圖象如圖
該圖象是由拋物線y=x
2-5x+4將x軸下方的部分翻折到x軸上方
而x軸上方的部分不變而來的
直線y=k(x-

)是一條經過點(2.5,0)的直線
觀察圖象不難發現,當k=0時,兩曲線交點
為(1,0)和(4,0),兩個交點
而k>0或k<0時,均可得到兩曲線在x軸上方有兩個公共點
因此可得,不論k是正數、負數還是0,均可得到兩曲線有兩個公共點
故選B
點評:本題考查了函數與方程根的個數問題,屬于基礎題.數形結合是此類問題的常用方法,本題還考查了直線方程的基本量的特性,是一道不錯的考題.

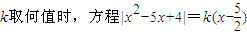 的實根個數是( )
的實根個數是( ) 解:記f(x)=|x2-5x+4|,作出它的圖象如圖
解:記f(x)=|x2-5x+4|,作出它的圖象如圖 )是一條經過點(2.5,0)的直線
)是一條經過點(2.5,0)的直線

 閱讀快車系列答案
閱讀快車系列答案