
【題目】如圖,四棱錐S—ABCD的底面是正方形,側棱SA⊥底面ABCD,
過A作AE垂直SB交SB于E點,作AH垂直SD交SD于H點,平面AEH交SC于K點,且AB=1,SA=2.

(1)證明E、H在以AK為直徑的圓上,且當點P是SA上任一點時,試求![]() 的最小值;
的最小值;
(2)求平面AEKH與平面ABCD所成的銳二面角的余弦值.
【答案】(1)見解析;(2)![]()
【解析】
(1)將側面![]() 繞側棱
繞側棱![]() 旋轉到與側面
旋轉到與側面![]() 在同一平面內,當
在同一平面內,當![]() 三點共線時,
三點共線時,![]() 取最小值,這時,
取最小值,這時,![]() 的最小值即線段
的最小值即線段![]() 的長,由此能求出結果;
的長,由此能求出結果;
(2)以A為原點,分別以AB、AD、AS所在的直線為x、y、z軸,建立空間直角坐標系,利用向量法能求出平面AEKH與平面ABCD所成銳二面角的余弦值.
(1)∵SA⊥底面ABCD,∴SA⊥BC,又AB⊥BC,
∴BC⊥平面SAB,又![]() 平面SAB,∴EA⊥BC,又∵AE⊥SB,∴AE⊥平面SBC ,
平面SAB,∴EA⊥BC,又∵AE⊥SB,∴AE⊥平面SBC ,
又![]() 平面SBC,∴EA⊥EK, 同理 AH⊥KH,
平面SBC,∴EA⊥EK, 同理 AH⊥KH,
∴E、H在以AK為直徑的圓上
現將側面SAB繞側棱SA旋轉到與側面SAD在同一平面內,如右圖示,

則當B、P、H三點共線時,![]() 取最小值,這時,
取最小值,這時,![]() 的
的
最小值即線段BH的長,設![]() ,則
,則![]() ,
,
在![]() 中,∵
中,∵![]() ,∴
,∴![]() ,
,
在三角形BAH中,有余弦定理得:
![]()
![]()
∴![]() .
.
(2)以A為原點,分別以AB、AD、AS所在的直線為x、y、z軸,建立空間直角坐標系,則S(0,0,2),C(1,1,0),由(1)可得AE⊥SC,AH⊥SC,
∴SC⊥平面AEKH,![]() 為平面AEKH的一個法向量,
為平面AEKH的一個法向量,
![]() 為平面ABCDF的一個法向量,設平面AEKH與平面ABCD所成的銳二面角的平面角為
為平面ABCDF的一個法向量,設平面AEKH與平面ABCD所成的銳二面角的平面角為![]() ,則
,則![]()
∴平面AEKH與平面ABCD所成的銳二面角的余弦值![]()


科目:高中數學 來源: 題型:
【題目】近年空氣質量逐步惡化,霧霾天氣現象增多,大氣污染危害加重.大氣污染可引起心悸、呼吸困難等心肺疾病.為了解某市心肺疾病是否與性別有關,在某醫院隨機對心肺疾病入院的![]() 人進行問卷調查,得到了如下的列聯表:
人進行問卷調查,得到了如下的列聯表:
患心肺疾病 | 不患心肺疾病 | 合計 | |
男 | A |
|
|
女 |
|
|
|
合計 |
| B |
|
(1)根據已知條件求出上面的![]() 列聯表中的A和B;用分層抽樣的方法在患心肺疾病的人群中抽
列聯表中的A和B;用分層抽樣的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)為了研究心肺疾病是否與性別有關,請計算出統計量![]() ,并說明是否有
,并說明是否有![]() 的把握認為心肺疾病與性別有關?
的把握認為心肺疾病與性別有關?
下面的臨界值表供參考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
參考公式: ![]() ,其中
,其中![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知圓C:(x﹣1)2+y2=r2(r>0)與直線l:y=x+3,且直線l有唯一的一個點P,使得過P點作圓C的兩條切線互相垂直,則r=;設EF是直線l上的一條線段,若對于圓C上的任意一點Q,∠EQF≥ ![]() ,則|EF|的最小值= .
,則|EF|的最小值= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為建立健全國家學生體質健康監測評價機制,激勵學生積極參加身體鍛煉,教育部印發《國家學生體質健康標準(2014年修訂)》,要求各學校每學期開展覆蓋本校各年級學生的《標準》測試工作,并根據學生每個學期總分評定等級.某校決定針對高中學生,每學期進行一次體質健康測試,以下是小明同學六個學期體質健康測試的總分情況.
學期 | 1 | 2 | 3 | 4 | 5 | 6 |
總分 | 512 | 518 | 523 | 528 | 534 | 535 |
(1)請根據上表提供的數據,用相關系數![]() 說明
說明![]() 與
與![]() 的線性相關程度,并用最小二乘法求出
的線性相關程度,并用最小二乘法求出![]() 關于
關于![]() 的線性回歸方程(線性相關系數保留兩位小數);
的線性回歸方程(線性相關系數保留兩位小數);
(2)在第六個學期測試中學校根據 《標準》,劃定540分以上為優秀等級,已知小明所在的學習小組10個同學有6個被評定為優秀,測試后同學們都知道了自己的總分但不知道別人的總分,小明隨機的給小組內4個同學打電話詢問對方成績,優秀的同學有![]() 人,求
人,求![]() 的分布列和期望.
的分布列和期望.
參考公式: 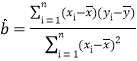 ,
,![]() ;
;
相關系數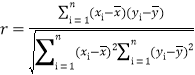 ;
;
參考數據:![]() ,
,![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() 的定義域
的定義域![]() ,值域是
,值域是![]() ;
;![]() 定義域
定義域![]() ,值域是
,值域是![]() ,其中實數
,其中實數![]() 滿足
滿足![]() .
.
甲:如果任意![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
乙:如果存在![]() ,存在
,存在![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丙:如果任意![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
丁:如果存在![]() ,任意
,任意![]() ,使得
,使得![]() ,那么
,那么![]() ;
;
請判斷上述四個命題中,假命題的個數是( )
A.0B.1C.2D.3
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】將2006表示成5個正整數![]() 之和. 記
之和. 記![]() . 問:
. 問:
(1)當![]() 取何值時,S取到最大值;
取何值時,S取到最大值;
(2)進一步地,對任意![]() 有
有![]() ,當
,當![]() 取何值時,S取到最小值. 說明理由.
取何值時,S取到最小值. 說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ;
;
(1)若函數![]() 在
在![]() 上為增函數,求正實數
上為增函數,求正實數![]() 的取值范圍;
的取值范圍;
(2)當![]() 時,求函數
時,求函數![]() 在
在![]() 上的最值;
上的最值;
(3)當![]() 時,對大于1的任意正整數
時,對大于1的任意正整數![]() ,試比較
,試比較![]() 與
與![]() 的大小關系.
的大小關系.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】下列命題中正確的命題是( )
A.若存在![]() ,當
,當![]() 時,有
時,有![]() ,則說函數
,則說函數![]() 在區間
在區間![]() 上是增函數:
上是增函數:
B.若存在![]() (
(![]() ,
,![]() ,
,![]() 、
、![]() ),當
),當![]() 時,有
時,有![]() ,則說函數
,則說函數![]() 在區間
在區間![]() 上是增函數;
上是增函數;
C.函數![]() 的定義域為
的定義域為![]() ,若對任意的
,若對任意的![]() ,都有
,都有![]() ,則函數
,則函數![]() 在
在![]() 上一定是減函數:
上一定是減函數:
D.若對任意![]() ,當
,當![]() 時,有
時,有![]() ,則說函數
,則說函數![]() 在區間
在區間![]() 上是增函數.
上是增函數.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數f(x)=a(x﹣1)2+lnx+1,g(x)=f(x)﹣x,其中a∈R.
(Ⅰ)當a=﹣ ![]() 時,求函數f(x)的極值;
時,求函數f(x)的極值;
(Ⅱ)當a>0時,求函數g(x)的單調區間;
(Ⅲ)當x∈[1,+∞)時,若y=f(x)圖象上的點都在 ![]() 所表示的平面區域內,求實數a的取值范圍.
所表示的平面區域內,求實數a的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com