
【題目】在平面直角坐標系![]() 中,曲線
中,曲線![]() 的參數方程為
的參數方程為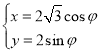 (
(![]() 為參數).以坐標原點為極點,
為參數).以坐標原點為極點,![]() 軸的正半軸為極軸,建立極坐標系,已知直線
軸的正半軸為極軸,建立極坐標系,已知直線![]() 的極坐標方程為
的極坐標方程為![]() .
.
(1)求曲線![]() 的普通方程和直線
的普通方程和直線![]() 的直角坐標方程;
的直角坐標方程;
(2)設![]() 為曲線
為曲線![]() 上的一個動點,求點
上的一個動點,求點![]() 到直線
到直線![]() 距離的最小值.
距離的最小值.
 芝麻開花課程新體驗系列答案
芝麻開花課程新體驗系列答案科目:高中數學 來源: 題型:
【題目】對于定義域為![]() 的函數
的函數![]() ,如果同時滿足以下三個條件:①任意的
,如果同時滿足以下三個條件:①任意的![]() ,總有
,總有![]() ;②
;②![]() ;③若
;③若![]() ,
,![]() ,
,![]() ,總有
,總有![]() 成立,則稱函數
成立,則稱函數![]() 為理想函數.
為理想函數.
(1)證明:若函數![]() 為理想函數,則
為理想函數,則![]() ;
;
(2)證明:函數![]() ,
,![]() 是理想函數;
是理想函數;
(3)證明:若函數![]() 為理想函數,假定存在
為理想函數,假定存在![]() ,使得
,使得![]() 且
且![]() ,則
,則![]() .
.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】選修4-4:坐標系與參數方程
已知曲線![]() 的參數方程是
的參數方程是![]() (
(![]() 為參數),以坐標原點為極點,
為參數),以坐標原點為極點,![]() 軸的正半軸為極軸建立極坐標系,曲線
軸的正半軸為極軸建立極坐標系,曲線![]() 的極坐標方程是
的極坐標方程是![]() .
.
(1)寫出![]() 的極坐標方程和
的極坐標方程和![]() 的直角坐標方程;
的直角坐標方程;
(2)已知點![]() 、
、![]() 的極坐標分別為
的極坐標分別為![]() 和
和![]() ,直線
,直線![]() 與曲線
與曲線![]() 相交于
相交于![]() ,
,![]() 兩點,射線
兩點,射線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,射線
,射線![]() 與曲線
與曲線![]() 相交于點
相交于點![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】為了保障某治療新冠肺炎藥品的主要藥理成分在國家藥品監督管理局規定的值范圍內,武漢某制藥廠在該藥品的生產過程中,檢驗員在一天中按照規定從該藥品生產線上隨機抽取20件產品進行檢測,測量其主要藥理成分含量(單位:mg).根據生產經驗,可以認為這條藥品生產線正常狀態下生產的產品的主要藥理成分含量服從正態分布N(μ,σ2).在一天內抽取的20件產品中,如果有一件出現了主要藥理成分含量在(μ﹣3σ,μ+3σ)之外的藥品,就認為這條生產線在這一天的生產過程可能出現了異常情況,需對本次的生產過程進行檢查.
(1)下面是檢驗員在2月24日抽取的20件藥品的主要藥理成分含量:
10.02 | 9.78 | 10.04 | 9.92 | 10.14 | 10.04 | 9.22 | 10.13 | 9.91 | 9.95 |
10.09 | 9.96 | 9.88 | 10.01 | 9.98 | 9.95 | 10.05 | 10.05 | 9.96 | 10.12 |
經計算得![]() xi=9.96,s
xi=9.96,s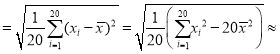 0.19;其中xi為抽取的第i件藥品的主要藥理成分含量,i=1,2,…,20.用樣本平均數
0.19;其中xi為抽取的第i件藥品的主要藥理成分含量,i=1,2,…,20.用樣本平均數![]() 作為μ的估計值
作為μ的估計值![]() ,用樣本標準差s作為σ的估計值
,用樣本標準差s作為σ的估計值![]() ,利用估計值判斷是否需對本次的生產過程進行檢查?
,利用估計值判斷是否需對本次的生產過程進行檢查?
(2)假設生產狀態正常,記X表示某天抽取的20件產品中其主要藥理成分含量在(μ﹣3σ,μ+3σ)之外的藥品件數,求/span>P(X=1)及X的數學期望.
附:若隨機變量Z服從正態分布N(μ,σ2),則P(μ﹣3σ<Z<μ+3σ)≈0.9974,0.997419≈0.95.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】關于圓周率π,數學發展史上出現過許多很有創意的求法,如著名的蒲豐實驗和查理斯實驗,受其啟發,我們也可以通過設計下面的實驗來估計π的值,先請240名同學,每人隨機寫下兩個都小于1的正實數x,y組成的實數對(x,y);若將(x,y)看作一個點,再統計點(x,y)在圓x2+y2=1外的個數m;最后再根據統計數m來估計π的值,假如統計結果是m=52,那么可以估計π的近似值為_______.(用分數表示)
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,四棱錐PABC中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M為線段AD上一點,AM=2MD,N為PC的中點.

(Ⅰ)證明MN∥平面PAB;
(Ⅱ)求直線AN與平面PMN所成角的正弦值.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】已知函數![]() ,
,![]() 、
、![]() 、
、![]() ,且
,且![]() 都有
都有![]() ,滿足
,滿足![]() 的實數
的實數![]() 有且只有
有且只有![]() 個,給出下述四個結論:
個,給出下述四個結論:
①滿足題目條件的實數![]() 有且只有
有且只有![]() 個;②滿足題目條件的實數
個;②滿足題目條件的實數![]() 有且只有
有且只有![]() 個;
個;
③![]() 在
在![]() 上單調遞增;④
上單調遞增;④![]() 的取值范圍是
的取值范圍是![]() .
.
其中所有正確結論的編號是( )
A.①④B.②③C.①②③D.①③④
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】“生命重于泰山,疫情就是命令,防控就是責任”.面對疫情,為切實做好防控,落實“停課不停學”,某校高三年級啟動線上公益學習活動,助“戰”高考.為了解學生的學習效果,李華老師在任教的甲、乙兩個班中各隨機抽取20名學生進行一次檢測,根據他們取得的成績(單位:分,滿分100分)繪制了如下莖葉圖,記成績不低于70分者為“成績優良”.
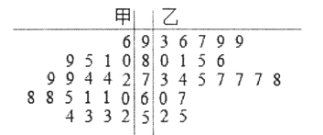
(1)分別估計甲、乙兩個班“成績優良”的概率;
(2)根據莖葉圖判斷哪個班的學習效果更好?并從兩個角度來說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com