
【題目】已知函數g(x)= ![]() +g(x).
+g(x).
(1)試判斷g(x)的單調性;
(2)若f(x)在區間(0,1)上有極值,求實數a的取值范圍;
(3)當a>0時,若f(x)有唯一的零點x0 , 試求[x0]的值.(注:[x]為取整函數,表示不超過x的最大整數,如[0.3]=0,[2.6]=2,[﹣1.4]=﹣2;以下數據供參考:ln2=0.6931,ln3=1.099,ln5=1.609,ln7=1.946)
【答案】
(1)解: ![]() ,
, ![]()
② 當a≥0時,g'(x)<0,∴函數g(x)在區間(0,+∞)上單調遞減;
②當a<0時,由g'(x)=0,解得 ![]() ,
,
當 ![]() 時,g'(x)<0,此時函數g(x)單調遞減;
時,g'(x)<0,此時函數g(x)單調遞減;
當 ![]() 時,g'(x)>0,此時函數g(x)單調遞增
時,g'(x)>0,此時函數g(x)單調遞增
(2)解:f(x)=x2+g(x),其定義域為(0,+∞).
![]() ,
,
令h(x)=2x3﹣ax﹣2,x∈(0,+∞),h'(x)=6x2﹣a,
當a<0時,h'(x)>0恒成立,∴h(x)在(0,+∞)上為增函數,
又h(0)=﹣2<0,h(1)=﹣a>0,
∴函數h(x)在(0,1)內至少存在一個變號零點x0,且x0也是f'(x)的變號零點,
此時f(x)在區間(0,1)內有極值.
當a≥0時,h(x)=2(x3﹣1)﹣ax<0,即x∈(0,1)時,f'(x)<0恒成立,
∴函數f(x)在(0,1)單調遞減,此時函數f(x)無極值
綜上可得:f(x)在區間(0,1)內有極值時實數a的取值范圍是(﹣∞,0)
(3)解:∵a>0時,函數f(x)的定義域為(0,+∞)
由(2)可知:f(1)=3知x∈(0,1)時,f(x)>0,∴x0>1.
又f(x)在區間(1,+∞)上只有一個極小值點記為x1,
且x∈(1,x1)時,f'(x)<0,函數f(x)單調遞減,
x∈(x1,+∞)時,f'(x)>0,函數f(x)單調遞增,
由題意可知:x1即為x0.
∴ ![]() ,∴
,∴ 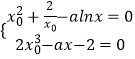 消去可得:
消去可得: ![]() ,
,
即 ![]()
令 ![]() ,則t(x)在區間(1,+∞)上單調遞增
,則t(x)在區間(1,+∞)上單調遞增
又∵ ![]()
![]()
由零點存在性定理知 t(2)<0,t(3)>0
∴2<x0<3∴[x0]=2
【解析】(1)求出g(x)的導數,討論當a≥0時,當a<0時,由導數大于0,可得增區間;導數小于0,可得減區間,注意定義域;(2)求出f(x)的導數,令h(x)=2x3﹣ax﹣2,x∈(0,+∞),求出導數,討論a的符號,判斷單調性,即可得到所求a的范圍;(3)由(2)可知:f(1)=3知x∈(0,1)時,f(x)>0,則x0>1,討論f(x)在x>1的單調性,再由零點的定義和極值點的定義,可得x0的方程,構造函數 ![]() ,判斷單調性,由零點存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
,判斷單調性,由零點存在性定理知 t(2)<0,t(3)>0,即可得到所求值.
【考點精析】認真審題,首先需要了解利用導數研究函數的單調性(一般的,函數的單調性與其導數的正負有如下關系: 在某個區間![]() 內,(1)如果
內,(1)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞增;(2)如果
在這個區間單調遞增;(2)如果![]() ,那么函數
,那么函數![]() 在這個區間單調遞減),還要掌握函數的極值與導數(求函數
在這個區間單調遞減),還要掌握函數的極值與導數(求函數![]() 的極值的方法是:(1)如果在
的極值的方法是:(1)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極大值(2)如果在
是極大值(2)如果在![]() 附近的左側
附近的左側![]() ,右側
,右側![]() ,那么
,那么![]() 是極小值)的相關知識才是答題的關鍵.
是極小值)的相關知識才是答題的關鍵.


 名校課堂系列答案
名校課堂系列答案科目:高中數學 來源: 題型:
【題目】正方形ADEF與梯形ABCD所在平面互相垂直,AD⊥CD,AB∥CD,AB=AD= ![]() CD=2,點M是EC中點. (Ⅰ)求證:BM∥平面ADEF;
CD=2,點M是EC中點. (Ⅰ)求證:BM∥平面ADEF;
(Ⅱ)求三棱錐M﹣BDE的體積.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖,橢圓E: ![]() ,點P(0,1)在短軸CD上,且
,點P(0,1)在短軸CD上,且 ![]()
(Ⅰ) 求橢圓E的方程及離心率;
(Ⅱ) 設O為坐標原點,過點P的動直線與橢圓交于A,B兩點.是否存在常數λ,使得 ![]() 為定值?若存在,求λ的值;若不存在,請說明理由.
為定值?若存在,求λ的值;若不存在,請說明理由.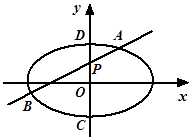
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若a1=1,對任意的n∈N* , 都有an>0,且nan+12﹣(2n﹣1)an+1an﹣2an2=0設M(x)表示整數x的個位數字,則M(a2017)= .
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】若四面體ABCD的三組對棱分別相等,即AB=CD,AC=BD,AD=BC,則(寫出所有正確結論編號) ①四面體ABCD每組對棱相互垂直
②四面體ABCD每個面的面積相等
③從四面體ABCD每個頂點出發的三條棱兩兩夾角之和大于90°而小于180°
④連接四面體ABCD每組對棱中點的線段互垂直平分
⑤從四面體ABCD每個頂點出發的三條棱的長可作為一個三角形的三邊長.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】如圖1,四邊形ABCD為直角梯形,AD∥BC,AD⊥AB,AD=1,BC=2,E為CD上一點,F為BE的中點,且DE=1,EC=2,現將梯形沿BE折疊(如圖2),使平面BCE⊥ABED.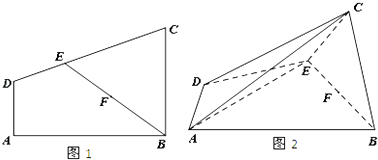
(1)求證:平面ACE⊥平面BCE;
(2)能否在邊AB上找到一點P(端點除外)使平面ACE與平面PCF所成角的余弦值為 ![]() ?若存在,試確定點P的位置,若不存在,請說明理由.
?若存在,試確定點P的位置,若不存在,請說明理由.
查看答案和解析>>
科目:高中數學 來源: 題型:
【題目】設橢圓C: ![]() =1(a>b>0),橢圓C短軸的一個端點與長軸的一個端點的連線與圓O:x2+y2=
=1(a>b>0),橢圓C短軸的一個端點與長軸的一個端點的連線與圓O:x2+y2= ![]() 相切,且拋物線y2=﹣4
相切,且拋物線y2=﹣4 ![]() x的準線恰好過橢圓C的一個焦點. (Ⅰ)求橢圓C的方程;
x的準線恰好過橢圓C的一個焦點. (Ⅰ)求橢圓C的方程;
(Ⅱ)過圓O上任意一點P作圓的切線l與橢圓C交于A,B兩點,連接PO并延長交圓O于點Q,求△ABQ面積的取值范圍.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com